题目内容
已知函数![]()
![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围。
的取值范围。
解:(Ⅰ)![]() .
.
①当![]() 时,由于
时,由于![]() ,故
,故![]() ,
,![]()
所以,![]() 的单调递增区间为
的单调递增区间为![]()
②当![]() 时,由
时,由![]() ,得
,得![]() .
.
在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上
上![]() ,
,
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)由已知,转化为![]() .
.
![]()
由(Ⅱ)知,当![]() 时,
时,![]() 在
在![]() 上单调递增,值域为
上单调递增,值域为![]() ,故不符合题意.
,故不符合题意.
(或者举出反例:存在![]() ,故不符合题意.)
,故不符合题意.)
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() 的极大值即为最大值,
的极大值即为最大值,![]() ,
,
所以![]() ,
,
解得![]() .
.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.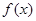 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求