题目内容
设数列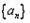
的前n项和为Sn，满足
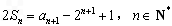，且
、
、
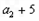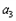成等差数列。
（Ⅰ）求a1的值；
（Ⅱ）求数列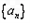
的通项公式；
（Ⅲ）证明：对一切正整数n，有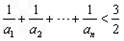
。
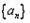的前n项和为Sn，满足
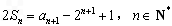，且
、
、
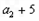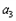成等差数列。（Ⅰ）求a1的值；
（Ⅱ）求数列
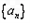的通项公式；（Ⅲ）证明：对一切正整数n，有
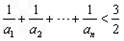。解析：（Ⅰ）由
，解得
。
（Ⅱ）由
可得
（
），
两式相减，可得
，即
，
即
，
所以数列
（
）是一个以
为首项，3为公比的等比数列
由
可得，
，
所以
，即
（
），
当
时，
，也满足该式子，
所以数列
的通项公式是
。
（Ⅲ）因为
，
所以
，
所以
，
于是
。
，解得
。（Ⅱ）由
可得
（
），两式相减，可得
，即
，即
，所以数列
（
）是一个以
为首项，3为公比的等比数列由
可得，
，所以
，即
（
），当
时，
，也满足该式子，所以数列
的通项公式是
。（Ⅲ）因为
，所以
，所以
，于是
。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，其前n项和Sn满足
是大于0的
的值；
的前n项和为Tn，试比较
与Sn的大小.
的前n项和为S??n，点
的直线
上，数列
满足
，
，且
的通项公式；（Ⅱ）设
，记数列
的前n项和为Tn，求使不等式
对一切
都成立的最大正整数k的值.