题目内容
(本小题满分12分)设向量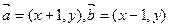 ,点
,点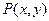 为动点,
为动点, 已知
已知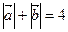 。
。
(1)求点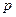 的轨迹方程;
的轨迹方程;
(2)设点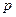 的轨迹与
的轨迹与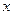 轴负半轴交于点
轴负半轴交于点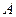 ,过点
,过点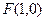 的直线交点
的直线交点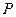 的轨迹于
的轨迹于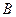 、
、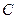 两点,试推断
两点,试推断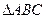 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
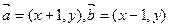 ,点
,点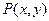 为动点,
为动点, 已知
已知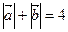 。
。(1)求点
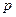 的轨迹方程;
的轨迹方程;(2)设点
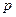 的轨迹与
的轨迹与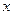 轴负半轴交于点
轴负半轴交于点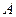 ,过点
,过点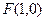 的直线交点
的直线交点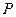 的轨迹于
的轨迹于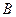 、
、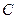 两点,试推断
两点,试推断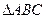 的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。
的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由。(1)动点P的轨迹 方程是
方程是
(2)三角形的面积最大值为
 方程是
方程是
(2)三角形的面积最大值为

解:(1)由已知, ,所以动点P的轨迹M
,所以动点P的轨迹M
是以点 为焦点,长轴长为4的椭圆。因为
为焦点,长轴长为4的椭圆。因为 ,则
,则 。故动点P的轨迹
。故动点P的轨迹 方程是
方程是 ---------------4分
---------------4分
(2) 设直线BC的方程 (1)
(1)
 (2) 可得
(2) 可得 ,
,
设点 则
则 ,-----------3分
,-----------3分
所以 =
= ------------1分
------------1分
点A到直线BC的距离 ----------1分
----------1分
 -------------1分
-------------1分
令

故三角形的面积最大值为 ----------------2分
----------------2分
 ,所以动点P的轨迹M
,所以动点P的轨迹M是以点
 为焦点,长轴长为4的椭圆。因为
为焦点,长轴长为4的椭圆。因为 ,则
,则 。故动点P的轨迹
。故动点P的轨迹 方程是
方程是 ---------------4分
---------------4分(2) 设直线BC的方程
 (1)
(1)  (2) 可得
(2) 可得 ,
, 设点
 则
则 ,-----------3分
,-----------3分所以
 =
= ------------1分
------------1分点A到直线BC的距离
 ----------1分
----------1分 -------------1分
-------------1分 令


故三角形的面积最大值为
 ----------------2分
----------------2分
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
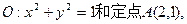 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足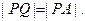
 ,(t>0)是角
,(t>0)是角 终边上的一点,则当
终边上的一点,则当 最小时,
最小时, ( )
( )



 中
中 ,点P是AB上一点,且
,点P是AB上一点,且 Q是BC中点,AQ与CP交点为M,又
Q是BC中点,AQ与CP交点为M,又 ,则
,则 的值为 ( )
的值为 ( )



 ( )
( ) =
=




 ,AD为BC边上的高,O为AD的中点,若
,AD为BC边上的高,O为AD的中点,若 = .
= . , 点
, 点
 在由射线
在由射线 、线段
、线段 及
及 的延长线围成的区域内
的延长线围成的区域内 
 ,则
,则 的取值范围是__________; 当
的取值范围是__________; 当 时,
时,  的取值范围是__________.
的取值范围是__________. 

 中,D、E分别是AB、AC的中点,DM=
中,D、E分别是AB、AC的中点,DM= DE,若
DE,若 ,
,
 表示
表示
 ,
, 是非零向量,且
是非零向量,且 的夹角为
的夹角为 ,则向量
,则向量 的模为 .
的模为 .