题目内容
已知函数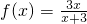
，数列{xn}满足x1=1，xn+1=f（xn），n∈N*
（1）求数列{xn}的通项公式．
（2）记an=xnxn+1，Sn=a1+a2+…+an，n∈N*，求证：Sn＜3．
解：（1）由题意，
由得
∴
（4分）
于是数列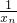
是以公差为
的等差数列，且首项为1，
故
，
所以
． （8分）
证明：（2）
（11分）
∴
=
（15分）
分析：（1）先由f（x）的式子给出xn+1的表达式，然后变形得出表达式
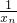，再用等差数列的定义得出数列是以公差为的等差数列，最后由等差数列的通项公式给出{xn}的表达式；
（2）先求出an，用拆项求和的方法进行求和式，根据变量n的范围进行放缩，最后从所得范围中证得结论．
点评：本题综合了函数、数列、不等式三个常见考点，属于难题．第一小问构造一个等差数列，抓住函数的表达式是解题的关键；第二小问求证不等式，注意运用拆项求和的方法进行解答．
由
得∴
（4分）于是数列
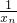是以公差为的等差数列，且首项为1，故
，所以
． （8分）证明：（2）
（11分）∴
=
（15分）分析：（1）先由f（x）的式子给出xn+1的表达式，然后变形得出表达式
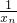，再用等差数列的定义得出数列是以公差为的等差数列，最后由等差数列的通项公式给出{xn}的表达式；（2）先求出an，用拆项求和的方法进行求和式，根据变量n的范围进行放缩，最后从所得范围中证得结论．
点评：本题综合了函数、数列、不等式三个常见考点，属于难题．第一小问构造一个等差数列，抓住函数的表达式是解题的关键；第二小问求证不等式，注意运用拆项求和的方法进行解答．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
=1按向量a=(t-3,t2)(t∈R)平移后得到曲线E,设曲线E的右焦点为P.
),且
(m∈R),求∠AOB(O为坐标原点)的最大值.
，数列{xn}满足x1=1，xn+1=f（xn），n∈N*
，数列{xn}满足x1=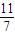
，xn+1=f（xn）；若bn=
．
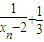，数列{xn}中，xn=f(xn-1)，若
，则x100=（ ）。