题目内容
已知函数
，数列{xn}满足x1=
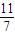，xn+1=f（xn）；若bn=
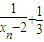．（1）求证数列{bn}是等比数列，并求其通项公式；
（2）若cn=3n-λbn（λ为非零整数，n∈N*），试确定λ的值，使得对任意n∈N*，都有cn+1＞cn成立．
【答案】分析：（1）先由f（x）的式子给出xn+1的表达式，然后由bn的式子给出bn+1的表达式，再用等比数列的定义证出
是一个常数，最后由等比数列的通项公式给出bn的表达式；
（2）用作差的方法得到一个关于λ和n的不等式，根据变量n的奇偶性将不等式分为两种情况进行讨论，得出λ的范围，最后从所得范围中找出λ的整数值．
解答：解：（1）由已知，
，
∴
=-2，（4分）
∴{bn}是等比数列，且q=-2；又
，∴bn=（-2）n．（6分）
（2）要使cn+1＞cn恒成立，
即要cn+1-cn=[3n+1-λ（-2）n+1]-[3n-λ（-2）n]=2•3n+3λ（-2）n＞0恒成立，
即要
恒成立．下面分n为奇数、n为偶数讨论：（8分）
①当n为奇数时，即
恒成立．又
的最小值为1．∴λ＜1．
②当n为偶数时，即
恒成立，又
的最大值为-
，∴λ＞-
．
综上，
，又λ为非零整数，
∴λ=-1时，使得对任意n∈N*，都有cn+1＞cn成立．（14分）
点评：本题综合了函数、数列、不等式三个常见考点，属于难题．第一小问证明等比数列，抓住函数的表达式是解题的关键；第二小问求参数λ的范围，注意运用变量分离的方法，结合分类讨论的思想进行解答．
是一个常数，最后由等比数列的通项公式给出bn的表达式；（2）用作差的方法得到一个关于λ和n的不等式，根据变量n的奇偶性将不等式分为两种情况进行讨论，得出λ的范围，最后从所得范围中找出λ的整数值．
解答：解：（1）由已知，
，∴
=-2，（4分）∴{bn}是等比数列，且q=-2；又
，∴bn=（-2）n．（6分）（2）要使cn+1＞cn恒成立，
即要cn+1-cn=[3n+1-λ（-2）n+1]-[3n-λ（-2）n]=2•3n+3λ（-2）n＞0恒成立，
即要
恒成立．下面分n为奇数、n为偶数讨论：（8分）①当n为奇数时，即
恒成立．又的最小值为1．∴λ＜1．②当n为偶数时，即
恒成立，又的最大值为-，∴λ＞-．综上，
，又λ为非零整数，∴λ=-1时，使得对任意n∈N*，都有cn+1＞cn成立．（14分）
点评：本题综合了函数、数列、不等式三个常见考点，属于难题．第一小问证明等比数列，抓住函数的表达式是解题的关键；第二小问求参数λ的范围，注意运用变量分离的方法，结合分类讨论的思想进行解答．
练习册系列答案
相关题目
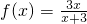，数列{xn}满足x1=1，xn+1=f（xn），n∈N*
=1按向量a=(t-3,t2)(t∈R)平移后得到曲线E,设曲线E的右焦点为P.
),且
(m∈R),求∠AOB(O为坐标原点)的最大值.
，数列{xn}满足x1=1，xn+1=f（xn），n∈N*
，数列{xn}中，xn=f(xn-1)，若
，则x100=（ ）。