题目内容

5．函数f（x）=2x-$\sqrt{1-x}$的值域为（-∞，2]．

分析 根据1-x≥0便可求出x和$\sqrt{1-x}$的范围，从而得出2x和-$\sqrt{1-x}$的范围，这样即得出f（x）的范围，即得出函数f（x）的值域．

解答 解：1-x≥0；
∴x≤1，$\sqrt{1-x}≥0$；
∴$2x≤2，-\sqrt{1-x}≤0$；
∴f（x）≤2；
∴f（x）的值域为（-∞，2]．
故答案为：（-∞，2]．

点评 考查函数值域的概念，一次函数的值域，以及根据不等式的性质求函数值域的方法．

练习册系列答案
相关题目
15．（1）证明：$\sqrt{5}-\sqrt{10}＞\sqrt{3}-\sqrt{8}$
（2）已知a，b，c∈R+，且a+b+c=1，求证：$（\frac{1}{a}-1）（\frac{1}{b}-1）（\frac{1}{c}-1）≥8$．
16．已知圆C的标准方程为（x-5）2+（y-6）2=a2
（1）若点M（6，9）在圆上，求a的值；
（2）已知点P（3，3）和点Q（5，3）有一点在圆内，另一点在圆外，求a的取值范围．
13．已知函数ft（x）=（x-t）2-t（t∈R），设a＜b，f（x）=$\left\{\begin{array}{l}{f_a}（x），{f_a}（x）＜{f_b}（x）\\{f_b}（x），{f_a}（x）≥{f_b}（x）\end{array}$，若函数y=f（x）+x+a-b有三个零点，则b-a的值为2+$\sqrt{5}$．
20．已知函数y=$\frac{{\sqrt{1-x}}}{{{x^2}-4}}$，其定义域为（　　）
A．（-∞，1]B．（-∞，2]C．（-∞，-2）∪（-2，1]D．[1，2）∪（2，+∞）
10．对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；设函数f（x）的定义域为R+，且f（1）=3．
（Ⅰ）若（a，b）是f（x）的一个“P数对”，且f（2）=6，f（4）=9，求常数a，b的值；
（Ⅱ）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求k的值及f（x）在区间[1，2n）（n∈N*）上的最大值与最小值．
17．已知集合A={1，2，3，4}，B={x|x=2n，n∈A}，则A∩B=（　　）
A．{1，4}B．{1，3}C．{2，4}D．{2，3}
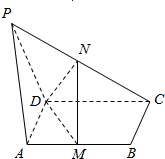14．已知集合P={x|x2-x-2≤0}，M={-1，0，3，4}，则集合P∩M中元素的个数为（　　）
A．1B．2C．3D．4
15．如图，PA⊥平面ABCD，ABCD是矩形，M、N分别是AB，PC的中点．
（1）求证：MN⊥AB；
（2）若PA=AD，求证：平面MND⊥平面PDC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网