题目内容
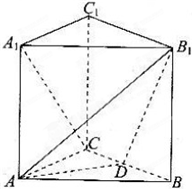 如图,在直三棱柱ABC-A1B1C1,AC⊥BC,AC=BC=BB1,点D是BC的中点.
如图,在直三棱柱ABC-A1B1C1,AC⊥BC,AC=BC=BB1,点D是BC的中点.
(1)求证:A1C∥平面AB1D;
(2)求二面角B1-AD-B的正弦值;
(3)判断在线段B1B上是否存在一点M,使得A1M⊥B1D?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
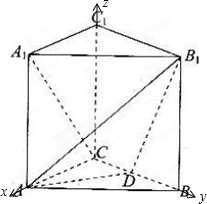 (1)证明:以C为坐标原点,建立如图所示的坐标系,
(1)证明:以C为坐标原点,建立如图所示的坐标系,设AC=BC=BB1=2,则A1(2,0,2),C(0,0,0),D(0,1,0),A(2,0,0),B1(0,2,2),B(0,2,0)
∴
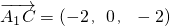 ,
,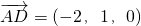 ,
,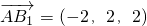
设平面AB1D的法向量为
 =(x,y,z),则由
=(x,y,z),则由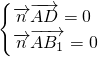 ,可得
,可得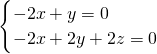 ,故可取
,故可取 =(1,2,-1)
=(1,2,-1)∵
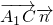 =0,∴A1C∥平面AB1D;
=0,∴A1C∥平面AB1D;(2)解:由(1)知平面AB1D的法向量为
 =(1,2,-1),平面ABD的法向量为
=(1,2,-1),平面ABD的法向量为 =(0,0,2)
=(0,0,2)∴二面角B1-AD-B的余弦值为|
 |=|
|=|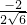 |
|∴二面角B1-AD-B的正弦值为
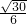 ;
;(3)解:设M(0,2,t),则
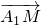 =(-2,2,t-2),
=(-2,2,t-2),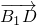 =(0,-1,-2)
=(0,-1,-2)若A1M⊥B1D,则
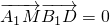 ,∴-2-2(t-2)=0,∴t=1
,∴-2-2(t-2)=0,∴t=1∴
 =1时,A1M⊥B1D.
=1时,A1M⊥B1D.分析:(1)以C为坐标原点,建立如图所示的坐标系,求出面AB1D的法向量,证明
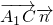 =0,即可得到结论;
=0,即可得到结论;(2)确定平面AB1D的法向量、平面ABD的法向量,利用向量的夹角公式,即可求得结论;
(3)设出M的坐标,利用则
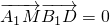 ,可得结论.
,可得结论.点评:本题考查线面平行,考查面面角,考查向量知识的运用,解题的关键是正确建立坐标系,属于中档题.

练习册系列答案
相关题目




