题目内容
设A,B,C,D是平面α内的四个定点,平面α内的点M满足
+
+
+
=
这样的点M的个数是( )
| MA |
| MB |
| MC |
| MD |
| 0 |
分析:设O为平面内任意一点,则
=
-
,
=
-
,
=
-
,
=
-
,可得4
=
+
+
+
,即满足条件的点M只有一个.
| MA |
| OA |
| OM |
| MB |
| OB |
| OM |
| MC |
| OC |
| OM |
| MD |
| OD |
| OM |
| OM |
| OA |
| OB |
| OC |
| OD |
解答:解:设O为平面内任意一点,则
=
-
,
=
-
,
=
-
,
=
-
,
∵
+
+
+
=
,∴4
=
+
+
+
设A、B、C、D四点的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)
由向量的坐标运算可得:点M的坐标为(
,
),
又A,B,C,D是平面α内的四个定点,即坐标为定定值,故点M的坐标也为定值,
所以点M为定点,即满足条件的点M只有一个.
故选B.
| MA |
| OA |
| OM |
| MB |
| OB |
| OM |
| MC |
| OC |
| OM |
| MD |
| OD |
| OM |
∵
| MA |
| MB |
| MC |
| MD |
| 0 |
| OM |
| OA |
| OB |
| OC |
| OD |
设A、B、C、D四点的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)
由向量的坐标运算可得:点M的坐标为(
| x1+x2+x3+x4 |
| 4 |
| y1+y2+y3+y4 |
| 4 |
又A,B,C,D是平面α内的四个定点,即坐标为定定值,故点M的坐标也为定值,
所以点M为定点,即满足条件的点M只有一个.
故选B.
点评:本题为向量的基本运算,把向量归结到以O为起点的向量是解决问题的关键,属基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
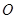 ,
, 为圆内异于
为圆内异于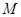 是圆周上一动点,把纸片折叠使
是圆周上一动点,把纸片折叠使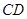 ,设
,设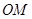 交于
交于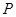 ,则
,则 ,是两个非零向量,如果
,是两个非零向量,如果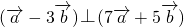 ,且
,且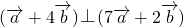 ,求向量
,求向量 与
与 的夹角大小;
的夹角大小;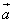 ,
,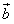 是两个非零向量,如果
是两个非零向量,如果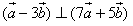 ,且
,且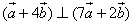 ,求向量
,求向量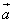 与
与 的夹角大小;
的夹角大小;