题目内容
(1)设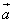 ,
,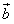 是两个非零向量,如果
是两个非零向量,如果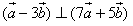 ,且
,且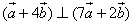 ,求向量
,求向量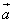 与
与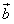 的夹角大小;
的夹角大小;
(2)用向量方法证明:设平面上A,B,C,D,四点满足条件AD⊥BC,BD⊥AC,则AB⊥CD。
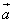 ,
,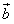 是两个非零向量,如果
是两个非零向量,如果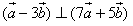 ,且
,且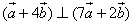 ,求向量
,求向量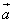 与
与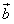 的夹角大小;
的夹角大小;(2)用向量方法证明:设平面上A,B,C,D,四点满足条件AD⊥BC,BD⊥AC,则AB⊥CD。
解:(1)因为
所以
因为
所以
两式相减得
于是
将 代回任一式得
代回任一式得
设 与
与 的夹角为
的夹角为 ,则
,则

所以 与
与 的夹角大小为
的夹角大小为 ;
;
(2)因为
所以
因为
所以
于是 ,
,
所以 ,
,
即
所以 ,即
,即 。
。

所以

因为

所以

两式相减得

于是

将
 代回任一式得
代回任一式得
设
 与
与 的夹角为
的夹角为 ,则
,则

所以
 与
与 的夹角大小为
的夹角大小为 ;
;(2)因为

所以

因为

所以

于是
 ,
,
所以
 ,
,
即

所以
 ,即
,即 。
。
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 ,是两个非零向量,如果
,是两个非零向量,如果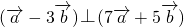 ,且
,且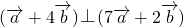 ,求向量
,求向量 与
与 的夹角大小;
的夹角大小;