题目内容
解不等式:lg(x2-3x)<1.
分析:根据对数函数的性质解对数不等式即可.
解答:解:∵y=lgx在(0,+∞)上单调递增,
∴不等式lg(x2-3x)<1.等价为:
,
得
,
∴-2<x<0,或3<x<5
故不等式的解集为(-2,0)∪(3,5)
∴不等式lg(x2-3x)<1.等价为:
|
得
|
∴-2<x<0,或3<x<5
故不等式的解集为(-2,0)∪(3,5)
点评:本题主要考查对数不等式的解法,利用对数函数的单调性和定义域是解决本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
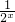 -2x,
-2x, )]>0.
)]>0.