题目内容
已知函数f(x)=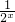 -2x,
-2x,
(1)若f(x)=2,求x的值;
(2)解关于x的不等式f[lg(x2-2)]+f[lg( )]>0.
)]>0.
解:(1)∵f(x)=2,∴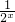 -2x=2,整理得(2x)2+2×2x-1=0
-2x=2,整理得(2x)2+2×2x-1=0
解得
∴x= …(4分)
…(4分)
(2)∵f(-x)=-f(x),∴f(x)是R上的奇函数
∵f[lg(x2-2)]+f[lg( )]>0
)]>0
∴f[lg(x2-2)]>f(lgx)
∵f′(x)=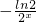 -2xln2<0
-2xln2<0
∴f(x)在R上为减函数,∴lg(x2-2)<lgx…(8分)
∴0<x2-2<x
∴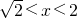 …(10分)
…(10分)
分析:(1)根据f(x)=2,可得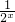 -2x=2,即(2x)2+2×2x-1=0,由此可求x的值;
-2x=2,即(2x)2+2×2x-1=0,由此可求x的值;
(2)判断f(x)是R上的奇函数、减函数,再将不等式转化为具体不等式,即可求得结论.
点评:本题考查指数方程,考查函数的单调性与奇偶性,考查不等式的解法,解题的关键是确定函数的性质,属于中档题.
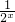 -2x=2,整理得(2x)2+2×2x-1=0
-2x=2,整理得(2x)2+2×2x-1=0解得

∴x=
 …(4分)
…(4分)(2)∵f(-x)=-f(x),∴f(x)是R上的奇函数
∵f[lg(x2-2)]+f[lg(
 )]>0
)]>0∴f[lg(x2-2)]>f(lgx)
∵f′(x)=
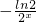 -2xln2<0
-2xln2<0∴f(x)在R上为减函数,∴lg(x2-2)<lgx…(8分)
∴0<x2-2<x
∴
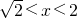 …(10分)
…(10分)分析:(1)根据f(x)=2,可得
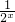 -2x=2,即(2x)2+2×2x-1=0,由此可求x的值;
-2x=2,即(2x)2+2×2x-1=0,由此可求x的值;(2)判断f(x)是R上的奇函数、减函数,再将不等式转化为具体不等式,即可求得结论.
点评:本题考查指数方程,考查函数的单调性与奇偶性,考查不等式的解法,解题的关键是确定函数的性质,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|