题目内容
（本小题满分14分，每小题7分)
（Ⅰ）设函数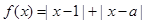
，如果
，
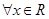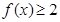，求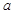
的取值范围．
（Ⅱ）用放缩法证明不等式：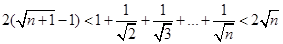
（Ⅰ）设函数
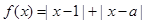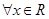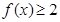，如果，，求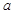的取值范围．（Ⅱ）用放缩法证明不等式：
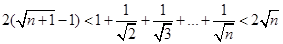
（1）
． （2）证明：见解析。
． （2）证明：见解析。(1)本小题属于绝对值不等式,要根据零点分段法,去掉绝对值,然后再解不等式.
(2)本小题证明利用不等式的放缩法.关键是
.
然后叠加即可.
解：（1）若
，
，不满足题设条件；…………………1分
若
，
，
的最小值为
；………………3分
若
，
，的最小值为
． ………………5分
所以对于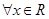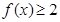，的充要条件是
，
故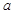的取值范围． ……………… 7分
（2）证明：
………………9分
………………12分
………………14分
(2)本小题证明利用不等式的放缩法.关键是
.然后叠加即可.
解：（1）若
，，不满足题设条件；…………………1分若
，，的最小值为；………………3分若
，，的最小值为． ………………5分所以对于
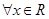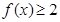，的充要条件是，故
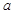的取值范围． ……………… 7分（2）证明：
………………9分 ………………12分 ………………14分
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
,则
（ ）
，则
的值为（ ）
其中n∈N，则f(8)等于（ ）
， 
的值；
时，求
取值的集合.
，则f(3)等于 （ ）
，则
.
，则
。
满足：x≥4,则
；当x＜4时
，则
＝( )
