题目内容
如图,在直角坐标系中,O为坐标原点,直线![]() ⊥x轴与点C,
⊥x轴与点C, ![]() ,
,![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是它到点D的距离的2倍。
的距离是它到点D的距离的2倍。
(I)求点![]() 的轨迹方程
的轨迹方程
(II)设点K为点![]() 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线![]() 交点
交点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 与点K不重合),且满足
与点K不重合),且满足![]() .动点
.动点![]() 满足
满足![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
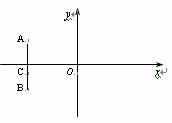
解: (I)依题意知,点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点、直线
为焦点、直线![]() 为其相应准线,离心率为
为其相应准线,离心率为![]() 的椭圆。设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
的椭圆。设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又![]() ,
,![]() ,∴点
,∴点![]() 在x轴上,且
在x轴上,且![]() ,则
,则![]() 3
3
解之得:![]() ,
,![]() .
.
∴坐标原点![]() 为椭圆的对称中心.
为椭圆的对称中心.
∴动点M的轨迹方程为:![]() .
.
(II)设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得
![]() .
.
![]() ,
,![]() .
.
![]()
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
解得:![]()
![]() (舍).
(舍).
设![]() ,由
,由![]() 知,
知,![]() .
.
直线![]() 的斜率为
的斜率为![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时, ,
,
![]() 时取“=”)或
时取“=”)或![]() 时取“=”),
时取“=”),
![]()
综上所述 

练习册系列答案
相关题目
 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: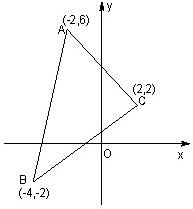 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与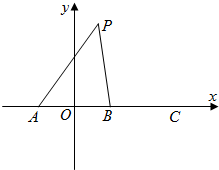 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m. 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为