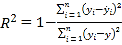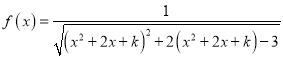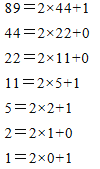题目内容
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线与函数
处的切线与函数![]() 的图象在
的图象在![]() 处的切线互相平行.
处的切线互相平行.
(1)求![]() 的值;
的值;
(2)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见详解
;(3)见详解
【解析】
(1)根据曲线在某点处的导数的几何意义,可得![]() 与函数
与函数![]() 的图象在
的图象在![]() 处的导数,由于切线平行,可得结果
处的导数,由于切线平行,可得结果
(2)利用分离参数的方法,得到![]() ,然后构建函数
,然后构建函数![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,根据
的单调性,根据![]() 的值域与
的值域与![]() 的大小关系,可得结果.
的大小关系,可得结果.
(3)根据(2),得到![]() ,然后令
,然后令![]() 代入,两边取对数,进行化简,结合不等式可得
代入,两边取对数,进行化简,结合不等式可得![]() ,最后求和可得结果.
,最后求和可得结果.
(1)由![]() ,所以
,所以![]() ,
,
则![]() ,又
,又![]()
所以![]() ,据题意可知:
,据题意可知:![]()
(2)由(1)可知![]()
又![]() 对
对![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,
恒成立,
令![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增,
单调递增,
所以![]()
所以![]()
所以实数![]() 的取值范围为
的取值范围为![]()
(3)由(2)可知:
当![]() 时,
时,![]() ,即
,即![]()
令![]() ,所以
,所以![]() ,两边取对数,
,两边取对数,
可得![]() ,
,
所以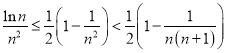
即![]()
所以
![]()
即![]()

练习册系列答案
相关题目
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).
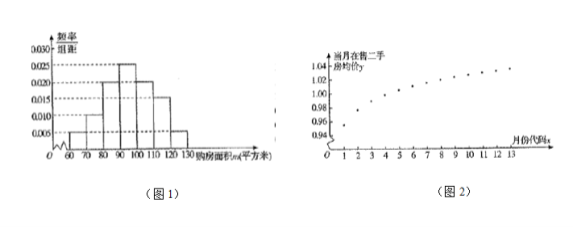
(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)现采用分层抽样的方法从购房面积位于![]() 的
的![]() 位市民中随机抽取
位市民中随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求这
人,求这![]() 人的购房面积恰好有一人在
人的购房面积恰好有一人在![]() 的概率;
的概率;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(参考公式)