题目内容
3.观察下列等式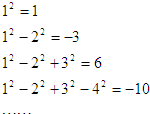
照此规律,第100个等式12-22+32-42+…-1002=-5050.
分析 观察可得:等式的左边是连续正整数的平方差相加的形式,根据这一规律得第100个等式左边为12-22+32-42+…+992-1002,利用分组求和法、等差数列的前n项和公式求出左边式子的和.
解答 解:观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10 …
当n=100时,左边=(12-22)+(32-42)+…+[(99)2-1002]
=-(3+7+11+199)=-$\frac{50(3+199)}{2}$=-5050,
故答案为:-5050.
点评 本题考查了归纳推理,以及分组求和法、等差数列的前n项和公式的应用,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
13.函数f(x)=$\sqrt{{x^2}+2x-3}$的递增区间为( )
| A. | [-1,+∞) | B. | [1,+∞) | C. | [-3,1] | D. | (-∞,-1] |
14.设函数f(x)=min{2$\sqrt{x}$,|x-2|},其中min|a,b|=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$.若函数y=f(x)-m有三个不同的零点x1,x2,x3,则x1+x2+x3的取值范围是( )
| A. | (2,6-2$\sqrt{3}$) | B. | (2,$\sqrt{3}$+1) | C. | (4,8-2$\sqrt{3}$) | D. | (0,4-2$\sqrt{3}$) |
11.记函数f(x)=1+$\frac{cosx}{1+sinx}$的所有正的零点从小到大依次为x1,x2,x3,…,若θ=x1+x2+x3+…x2015,则cosθ的值是( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
18.如图1是一个边长为1的正三角形,分别连接这个三角形三边中点,将在三角剖分成4个三角开(如图2),再分别连接图2中一个小三角形三边的中点,又可将原三角形剖分成7个三角形(如图3),…,依此类推,设第n个图中原三角形被剖分成an个三角形,则第4个图中最小三角形的边长为( );a100=( )
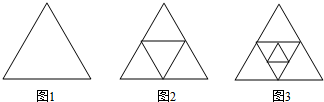

| A. | $\frac{1}{6}$,300 | B. | $\frac{1}{8}$,300 | C. | $\frac{1}{6}$,298 | D. | $\frac{1}{8}$,298 |
8.复数$\frac{a+i}{1+i}$为纯虚数,其中i为虚数单位,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |