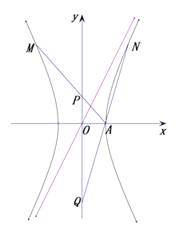
题目内容
【题目】已知椭圆![]()
![]() 的左右焦点分别是
的左右焦点分别是![]()
![]() ,
,![]() 是椭圆外的动点,满足
是椭圆外的动点,满足![]() .点
.点![]() 是线段
是线段![]() 与该椭圆的交点,点
与该椭圆的交点,点![]() 在线段
在线段![]() 上,并且满足
上,并且满足![]() ,
,![]() .
.
(1)当![]() 时,用点P的横坐标
时,用点P的横坐标![]() 表示
表示![]() ;
;
(2)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)在点![]() 的轨迹
的轨迹![]() 上,是否存在点
上,是否存在点![]() ,使
,使![]() 的面积
的面积![]() ?若存在,求出
?若存在,求出![]() 的正切值;若不存在,说明理由.
的正切值;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,正切值为2
;(3)存在,正切值为2
【解析】
(1)设出点的坐标,根据点在椭圆上,代入求解即可表示;
(2)根据几何意义求解轨迹方程;
(3)若存在点![]() ,使
,使![]() 的面积
的面积![]() ,即
,即![]() ,结合向量的数量及关系,表示面积关系得正切值.
,结合向量的数量及关系,表示面积关系得正切值.
(1)设点![]() 的坐标为
的坐标为![]() ,
,
由![]() 在椭圆上,得
在椭圆上,得 ,
,
由![]() ,知
,知![]() ,所以
,所以![]() .
.
(2)设点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,点
时,点![]() 和点
和点![]() 在轨迹上.
在轨迹上.
当![]() 且
且![]() 时,由
时,由![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() 为线段
为线段![]() 的中点.
的中点.
在![]() 中,
中,![]() ,所以有
,所以有![]() ,
,
综上所述,点![]() 的轨迹
的轨迹![]() 的方程是
的方程是![]() .
.
(3)![]() 上存在点
上存在点![]() 使
使![]() 的充要条件是
的充要条件是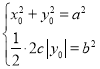 .
.
![]() ,
, ![]() ,所以当
,所以当![]() 时,存在点
时,存在点![]() ,使
,使![]() ;
;
当![]() 时,不存在满足条件的点
时,不存在满足条件的点![]() .
.
当![]() 时,
时,![]() ,
,
由![]() ,
,
![]() ,
,
所以![]() ,
,
![]() ,
,
即![]() ,
,
得![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目