题目内容
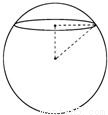
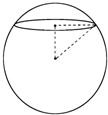 如图,用一平面去截球所得截面的面积为2πcm2,已知球心到该截面的距离为1cm,则该球的体积是
如图,用一平面去截球所得截面的面积为2πcm2,已知球心到该截面的距离为1cm,则该球的体积是
分析:求出小圆的半径,然后利用球心到该截面的距离为1 cm,小圆的半径,通过勾股定理求出球的半径,即可求出球的体积.
解答:解:用一平面去截球所得截面的面积为2π cm2,所以小圆的半径为:
cm;
已知球心到该截面的距离为1 cm,所以球的半径为:
=
所以球的体积为:
πr3=
π(
)3=4
π (cm3)
故答案为:4
π
| 2 |
已知球心到该截面的距离为1 cm,所以球的半径为:
12+(
|
| 3 |
所以球的体积为:
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题是基础题,考查球的小圆的半径,球心到该截面的距离,球的半径之间的关系,满足勾股定理,考查计算能力.

练习册系列答案
相关题目
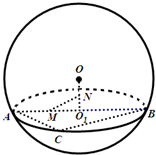 (2011•浦东新区三模)如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3cm,O1为截面小圆圆心,AB为截面小圆的直径.
(2011•浦东新区三模)如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3cm,O1为截面小圆圆心,AB为截面小圆的直径.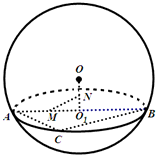 如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3cm,O1为截面小圆圆心,AB为截面小圆的直径.
如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3cm,O1为截面小圆圆心,AB为截面小圆的直径.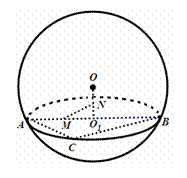 如图,用一平面去截球
如图,用一平面去截球