Question

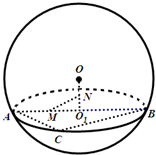（2011•浦东新区三模）如图，用一平面去截球O，所得截面面积为16π，球心O到截面的距离为3cm，O₁为截面小圆圆心，AB为截面小圆的直径．
（1）计算球O的表面积；
（2）若C是截面小圆上一点，∠ABC=30°，M、N分别是线段AO₁和OO₁的中点，求异面直线AC与MN所成的角（结果用反三角函数表示）．

Answer 1

分析：（1）求出小圆的半径，然后利用球心到该截面的距离为3cm，小圆的半径，通过勾股定理求出球的半径，即可求出球的表面积．
（2）由MN∥OA得，∠OAC为异面直线AC与MN所成的角（或补角），连接OC，然后利用余弦定理求出此角的余弦值，最后利用反三角表示出此角即可．

解答：解：（1）连接OA，由题意得，截面小圆半径为4cm（2分）
在Rt△OAO₁中，O₁A=4，OO₁=3，的由勾股定理知，AO=5，（4分）
所以，球O的表面积为：4π•25=100π（cm²）．（7分）
（2）由MN∥OA得，∠OAC为异面直线AC与MN所成的角（或补角）．（9分）
在Rt△ABC中，AB=8，∠ABC=30°，则AC=4，（10分）
连接OC，在△OAC中，OA=OC=5，由余弦定理知：cos∠OAC=

AC2+OA2-OC2

2OA•AC

=

42+52-52

2×4×5

=

2

5

，（12分）
故异面直线AC与MN所成的角为arccos

2

5

．（14分）

点评：本题主要考查了球的表面积，以及异面直线及其所成角和余弦定理的应用，属于中档题．