题目内容
设函数f(x)=tanx-8sinx,其中 .
.
(1)求函数f(x)的单调区间;
(2)若对 ,
, ,都有|f(x1)-f(x2)|≤a恒成立,求实数a的取值范围.
,都有|f(x1)-f(x2)|≤a恒成立,求实数a的取值范围.
解:(1)由f(x)=tanx-8sinx,得 ,
,
即 ,其中
,其中 ,解得,
,解得, ,
,
所以,函数f(x)的单调递增区间是: ,递减区间是
,递减区间是 .
.
(2)若对 ,
, ,都有|f(x1)-f(x2)|≤a恒成立,
,都有|f(x1)-f(x2)|≤a恒成立,
只需|f(x1)-f(x2)|max≤a.
由(1)得 f(x)在区间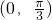 上单调递减,
上单调递减,
所以,当 时,-
时,- ≤f(x1)≤0,
≤f(x1)≤0,
同理,- ≤f(x2)≤0,
≤f(x2)≤0,
所以,- ≤f(x1)-f(x2)≤
≤f(x1)-f(x2)≤ ,
,
所以0≤|f(x1)-f(x2)|≤ ,
,
所以|f(x1)-f(x2)|max= ,
,
所以,a≥ .
.
分析:(1)求导函数,利用导数的正负可得函数的单调区间;
(2)对 ,
, ,都有|f(x1)-f(x2)|≤a恒成立,等价于|f(x1)-f(x2)|max≤a,由此可求实数a的取值范围.
,都有|f(x1)-f(x2)|≤a恒成立,等价于|f(x1)-f(x2)|max≤a,由此可求实数a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.
 ,
,即
 ,其中
,其中 ,解得,
,解得, ,
,所以,函数f(x)的单调递增区间是:
 ,递减区间是
,递减区间是 .
.(2)若对
 ,
, ,都有|f(x1)-f(x2)|≤a恒成立,
,都有|f(x1)-f(x2)|≤a恒成立,只需|f(x1)-f(x2)|max≤a.
由(1)得 f(x)在区间
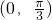 上单调递减,
上单调递减,所以,当
 时,-
时,- ≤f(x1)≤0,
≤f(x1)≤0,同理,-
 ≤f(x2)≤0,
≤f(x2)≤0,所以,-
 ≤f(x1)-f(x2)≤
≤f(x1)-f(x2)≤ ,
,所以0≤|f(x1)-f(x2)|≤
 ,
,所以|f(x1)-f(x2)|max=
 ,
,所以,a≥
 .
.分析:(1)求导函数,利用导数的正负可得函数的单调区间;
(2)对
 ,
, ,都有|f(x1)-f(x2)|≤a恒成立,等价于|f(x1)-f(x2)|max≤a,由此可求实数a的取值范围.
,都有|f(x1)-f(x2)|≤a恒成立,等价于|f(x1)-f(x2)|max≤a,由此可求实数a的取值范围.点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 已知抛物线C的顶点在原点,焦点坐标为F(2,0),点P的坐标为(m,0)(m≠0),设过点P的直线l交抛物线C于A,B两点,点P关于原点的对称点为点Q.
已知抛物线C的顶点在原点,焦点坐标为F(2,0),点P的坐标为(m,0)(m≠0),设过点P的直线l交抛物线C于A,B两点,点P关于原点的对称点为点Q.