题目内容
(本小题满分12分)
设函数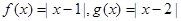 .
.
(Ⅰ)解不等式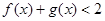 ;
;
(Ⅱ)对于实数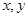 ,若
,若 ,求证
,求证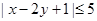 .
.
设函数
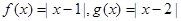 .
. (Ⅰ)解不等式
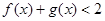 ;
;(Ⅱ)对于实数
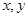 ,若
,若 ,求证
,求证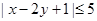 .
.(Ⅰ)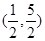 . (Ⅱ)
. (Ⅱ)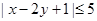 ,当且仅当
,当且仅当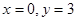 时取“=” 。
时取“=” 。
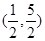 . (Ⅱ)
. (Ⅱ)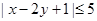 ,当且仅当
,当且仅当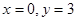 时取“=” 。
时取“=” 。本试题主要是考查了分段函数的性质和绝对值的求解的综合运用。
(1)因为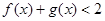 ,那么去掉绝对值符号可知不等式的解集。
,那么去掉绝对值符号可知不等式的解集。
(2)因为
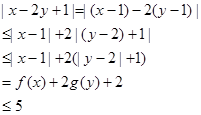 因此得到结论。
因此得到结论。
解: (Ⅰ)令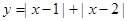 ,则
,则
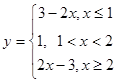
作出函数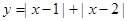 的图象,
的图象,
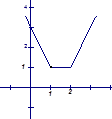
它与直线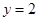 的交点为
的交点为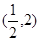 和
和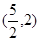 .
.
所以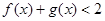 的解集为
的解集为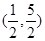 .------------6分
.------------6分
(Ⅱ)因为
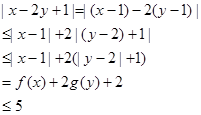
所以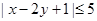
当且仅当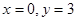 时取“=” …………………12分
时取“=” …………………12分
(1)因为
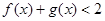 ,那么去掉绝对值符号可知不等式的解集。
,那么去掉绝对值符号可知不等式的解集。(2)因为
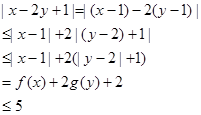 因此得到结论。
因此得到结论。解: (Ⅰ)令
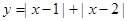 ,则
,则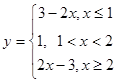
作出函数
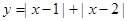 的图象,
的图象,
它与直线
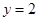 的交点为
的交点为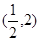 和
和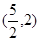 .
.所以
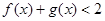 的解集为
的解集为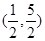 .------------6分
.------------6分(Ⅱ)因为
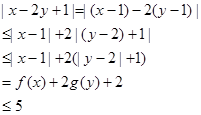
所以
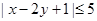
当且仅当
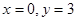 时取“=” …………………12分
时取“=” …………………12分
练习册系列答案
相关题目
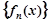 满足:
满足: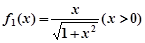 ,
,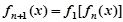
 ;
;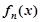 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论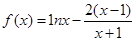 。
。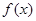 的单调性;
的单调性;
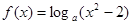 , 若
, 若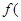 2)=1,求
2)=1,求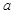 的值;
的值;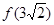 的值;
的值;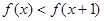 的解集.
的解集.
 成立,求实数a的取值范围;
成立,求实数a的取值范围; 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.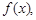 若存在
若存在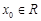 ,使
,使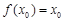 成立,则称点
成立,则称点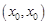 为函数的不动点,对于任意实数
为函数的不动点,对于任意实数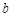 ,函数
,函数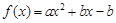 总有相异不动点,实数
总有相异不动点,实数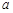 的取值范围是____
的取值范围是____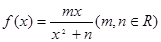 在
在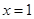 处取到极值
处取到极值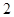
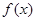 的解析式;
的解析式;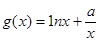 ,若对任意的
,若对任意的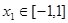 ,总存在
,总存在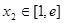 ,使得
,使得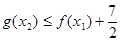 ,求实数
,求实数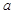 的取值范围.
的取值范围.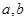 的代数式为
的代数式为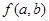 ,它满足关系:
,它满足关系: ; ②
; ②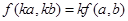 ;
; 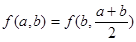 ;④
;④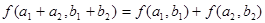 ,
,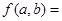 ( )
( )