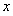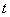Question

如图，从边长为的正方形铁皮的四个角各截去一个边长为的小正方形，再将四边向上折起，做成一个无盖的长方体铁盒，且要求长方体的高度与底面正方形的边长的比不超过常数，问：取何值时，长方体的容积V有最大值？

 

Answer 1

【答案】

略

【解析】此题是一道应用题，主要还是考查导数的定义及利用导数来求区间函数的最值，利用导数研究函数的单调性和极值、解不等式等基础知识，考查综合分析和解决问题的能力，解题的关键是求导要精确．

求体积最大值的问题，由题意解出v的表达式，对函数v进行求导，解出极值点，然后根据极值点来确定函数v的单调区间，

因极值点是关于a，t的表达式，此时就需要讨论函数v的单调性，分别代入求出最大值，从而求解．

解：长方体的体积V(x)＝4x(x－a)²，(o＜x＜a)，…………………………2分

由≤ t 得　0＜x≤< a  …………………4分

而V′＝12(x－)(x－a)   ∴V在（0，）增，在（， a）递减……………6分