Question

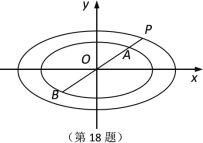
【题目】如图所示，在平面直角坐标系xOy中，已知椭圆C1：，椭圆C2：，C2与C1的长轴长之比为∶1，离心率相同．

（1）求椭圆C2的标准方程；

（2）设点为椭圆C2上一点．

① 射线与椭圆C1依次交于点，求证：为定值；

② 过点作两条斜率分别为的直线，且直线与椭圆C1均有且只有一个公共点，求证：为定值．

Answer 1

【答案】（1）；（2）①见解析，②见解析.

【解析】

（1）由题所求椭圆 a=,离心率，由得b即可；（2）①当直线OP斜率不存在时，得当直线OP斜率存在时，设直线OP的方程为，与椭圆联立，同理，推得从而可求；②设，直线的方程为 即，记，则的方程为，代入椭圆C1的方程得，由，得，再将代入得，同理，得到关于为根的方程，由韦达定理及点P在椭圆上化简即可求得为定值

（1）设椭圆C2的焦距为2c，由题意，，，，

解得，因此椭圆C2的标准方程为。

（2）①1°当直线OP斜率不存在时，

，，则．

2°当直线OP斜率存在时，设直线OP的方程为，

代入椭圆C1的方程，消去y，得，

所以，同理．

所以，由题意，同号，所以，

从而．

所以为定值．

②设，所以直线的方程为，即，记，则的方程为，

代入椭圆C1的方程，消去y，得，

因为直线与椭圆C1有且只有一个公共点，

所以，即，

将代入上式，整理得，，

同理可得，，

所以为关于k的方程的两根，

从而．又点在椭圆C2：上，所以，

所以为定值．