题目内容
 (2005•海淀区二模)如图所示,在△ABC中,AC=BC=1,∠ACB=90°,点D在斜边AB上,∠BCD=α(0<α<
(2005•海淀区二模)如图所示,在△ABC中,AC=BC=1,∠ACB=90°,点D在斜边AB上,∠BCD=α(0<α<| π |
| 2 |
(Ⅰ)求点Bn到平面ACD的距离(用α表示);
(Ⅱ)当AD⊥BnC时,求三棱锥Bn-ACD的体积;
(Ⅲ)当α=
| π |
| 3 |
分析:(I)作BnE⊥CD于E,利用平面和平面垂直的性质定理,证出BnE⊥平面ACD,BnE为所求.
(Ⅱ)当AD⊥BnC时,由(Ⅰ)中所作BnE⊥CD,得出
(Ⅱ)当AD⊥BnC时,由(Ⅰ)中所作BnE⊥CD,得出
解答:(本小题满分16分)
解:(I)作B'E⊥CD于E…(1分)
(II)∵BnE⊥平面ACD
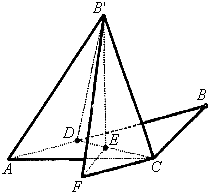
(文科)作EF⊥AC于F,连接BnF∵BnE⊥平面ACD,∴BnF⊥AC…(10分)∴∠BnFE为二面角Bn-AC-D的平面角…(11分)
在Rt△BnCE中,CE=BnC•cos
=
,BnE=BnC•sin
=
在Rt△CEF中,EF=CE•sin(
-
)=
•sin
=
,…(13分)
∴tan∠BnFE=
=2
…(16分)
即二面角Bn-AC-D的正切值为2
.
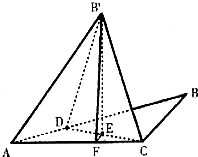
解:(I)作B'E⊥CD于E…(1分)
|
(II)∵BnE⊥平面ACD
|
|

(文科)作EF⊥AC于F,连接BnF∵BnE⊥平面ACD,∴BnF⊥AC…(10分)∴∠BnFE为二面角Bn-AC-D的平面角…(11分)
在Rt△BnCE中,CE=BnC•cos
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
|
| BnE |
| EF |
| 3 |
即二面角Bn-AC-D的正切值为2
| 3 |

点评:本题考查空间直线、平面位置关系的判断,空间角、体积求解,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目