题目内容
设等差数列 的公差为
的公差为 ,前
,前 项和为
项和为 .若
.若 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
B
解析试题分析:由题意得: ,所以
,所以
 当且仅当
当且仅当 时取等号.因此
时取等号.因此 的最小值为
的最小值为 .
.
考点:基本不等式求最值

练习册系列答案
相关题目
设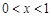 ,函数
,函数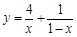 的最小值为( )
的最小值为( )
| A.10 | B.9 | C.8 | D.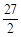 |
如果 ,
, ,则
,则 的最小值是 ( )
的最小值是 ( )
A. | B. | C.1+ | D.2- |
下列命题正确的是( )
A.若 ,则 ,则 | B.若 则 则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为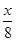 天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
| A.60件 | B.80件 | C.100件 | D.120件 |
若2x+2y=1,则x+y的取值范围是( )
| A.[0,2] | B.[﹣2,0] |
| C.[﹣2,+∞) | D.(﹣∞,﹣2] |
若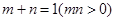 ,则
,则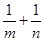 的最小值为( )
的最小值为( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
若a>0,b>0,且a+b=2,则下列不等式恒成立的是( )
A.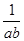 >1 >1 | B. + +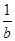 ≤2 ≤2 |
C. ≥1 ≥1 | D.a2+b2≥2 |
 (-6≤a≤3)的最大值为 ( ).
(-6≤a≤3)的最大值为 ( ).
| A.9 | B. | C.3 | D. |