题目内容
已知函数
的图象经过点
．
（Ⅰ）求
的表达式及其导数
；
（Ⅱ）求在闭区间
上的最大值和最小值．
的图象经过点．（Ⅰ）求
的表达式及其导数； （Ⅱ）求
在闭区间上的最大值和最小值．（Ⅰ）
，
（Ⅱ）最大值是
，最小值是
， （Ⅱ）最大值是，最小值是第一问由题意， ∴
∴
∴，
第二问令
∵
，
，，
∴在闭区间上的最大值是，最小值是．
∴ ∴∴
，第二问令
∵
，，，∴
在闭区间上的最大值是，最小值是．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
时，求不等式
的解集；
的解集包含
，求
的取值范围.
是偶函数，则函数图像与
轴交点的纵坐标的最大值是______．
是定义在
上的函数，其图象是一条连续的曲线，且满足下列条件：①
，
∈
|<|
立方米时，只付基本费9元和每户每月定额损耗费
元；
元的超额费；
（元）与月用水量
（立方米）的函数关系式；
的值。
，其长为32米，宽为18米，现要在此空地上种植一块矩形草坪，三边留有人行道，人行道宽度为
米与
米均不小于2米，且要求“转角处”（图中矩形
）的面积为8平方米
，并指出
上的函数
的图像关于
对称，且当
时，
（其中
是
的导函数），若
，则
的大小关系是 
,
，且
;
；
时,
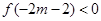恒成立,求实数
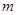的取值范围。
是定义在
上的增函数，函数
的图象关于
对称．若对任意的
，不等式
恒成立，则当
时，
的取值范围是 ．