题目内容
18.设m为实数,函数f(x)=2x2+(x-m)|x-m|,h(x)=$\left\{\begin{array}{l}{\frac{f(x)}{x},x≠0}\\{0,x=0}\end{array}\right.$.若h(x)对于一切x∈[1,3],不等式h(x)≥1恒成立,则实数m的取值范围是m≤2.分析 当x∈[1,3]时,h(x)=$\frac{2{x}^{2}+(x-m)|x-m|}{x}$,分类讨论以确定函数的单调性,从而求最值,化简恒成立问题为最值问题即可.
解答 解:当x∈[1,3]时,
f(x)=2x2+(x-m)|x-m|,
h(x)=$\frac{2{x}^{2}+(x-m)|x-m|}{x}$,
当m≤1时,
h(x)=$\frac{2{x}^{2}+(x-m)^{2}}{x}$=3x+$\frac{{m}^{2}}{x}$-2m
≥3+$\frac{{m}^{2}}{x}$-2m≥1,
故不等式h(x)≥1恒成立;
当1<m<3时,
h(x)=$\left\{\begin{array}{l}{x-\frac{{m}^{2}}{x}+2m,1≤x≤m}\\{3x+\frac{{m}^{2}}{x}-2m,m<x≤3}\end{array}\right.$,
由对勾函数的单调性及分段函数的单调性可知,
h(x)在[1,3]上单调递增,
故hmin(x)=h(1)=1-m2+2m≥1,
故0≤m≤2,
故1<m≤2;
当m≥3时,h(x)=x-$\frac{{m}^{2}}{x}$+2m在[1,3]上单调递增,
故hmin(x)=h(1)=1-m2+2m≥1,
故0≤m≤2,
故无解,
综上所述,m≤2.
故答案为:m≤2.
点评 本题考查了分段函数的应用及分类讨论的思想应用,关键在于化为最值问题.

练习册系列答案
相关题目
16.已知$\overrightarrow{a}$,$\overrightarrow{b}$是平面内互不相等的两个非零向量,且|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,则|$\overrightarrow{b}$|的取值范围是( )
| A. | (0,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | (0,2] | D. | [$\sqrt{3}$,2] |
8.设复数$z=\frac{-1+3i}{i}$(i为虚数单位)在复平面中对应点A,将OA绕原点O逆时针旋转θ角得到OB,若点B在第二象限,则θ角的可能值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
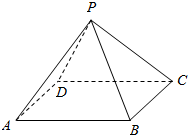 如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.
如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.