题目内容
设平面上向量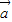 =(cosα,sinα)(0°≤α<360°),
=(cosα,sinα)(0°≤α<360°),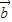 =(-
=(- ,
,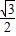 ).
).(1)试证:向量
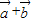 与
与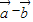 垂直;
垂直;(2)当两个向量
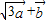 与
与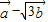 的模相等时,求角α.
的模相等时,求角α.
【答案】分析:(1)利用向量加减法的坐标运算求出向量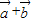 与
与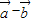 的坐标,由向量数量积的坐标运算化简可得向量
的坐标,由向量数量积的坐标运算化简可得向量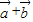 与
与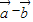 的数量积为0,则结论得证;
的数量积为0,则结论得证;
(2)利用向量的数乘运算和加减法运算求出向量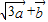 与
与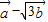 的坐标,由模相等得到模的平方向等,转化为向量的平方相等后展开整理,由三角函数的值及角的范围可得答案.
的坐标,由模相等得到模的平方向等,转化为向量的平方相等后展开整理,由三角函数的值及角的范围可得答案.
解答:(1)证明:因为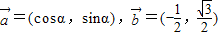 ,
,
所以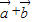 =
=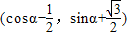 ,
,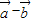 =
=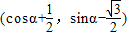 .
.
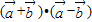 =
=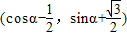 •
•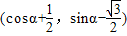
=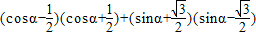
=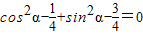 .
.
所以向量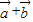 与
与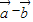 垂直;
垂直;
(2)解:由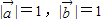 ,且
,且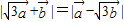 ,平方得
,平方得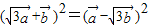 ,
,
整理得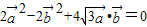 ,即
,即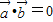 .
.
所以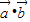 =
=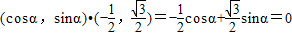 ,
,
即cos(60°+α)=0,或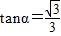 .
.
因为0°≤α<360°,所以α=30°或α=210°.
点评:本题考查向量的数量积判断两个向量的垂直关系,考查了数学转化思想方法,训练了三角函数的已知三角函数值求角的方法,考查了学生的计算能力,是中档题.
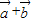 与
与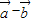 的坐标,由向量数量积的坐标运算化简可得向量
的坐标,由向量数量积的坐标运算化简可得向量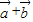 与
与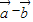 的数量积为0,则结论得证;
的数量积为0,则结论得证;(2)利用向量的数乘运算和加减法运算求出向量
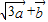 与
与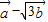 的坐标,由模相等得到模的平方向等,转化为向量的平方相等后展开整理,由三角函数的值及角的范围可得答案.
的坐标,由模相等得到模的平方向等,转化为向量的平方相等后展开整理,由三角函数的值及角的范围可得答案.解答:(1)证明:因为
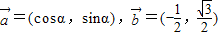 ,
,所以
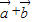 =
=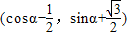 ,
,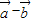 =
=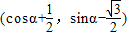 .
.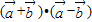 =
=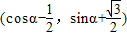 •
•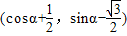
=
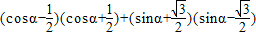
=
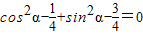 .
.所以向量
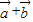 与
与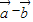 垂直;
垂直;(2)解:由
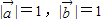 ,且
,且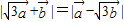 ,平方得
,平方得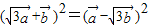 ,
,整理得
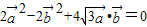 ,即
,即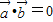 .
.所以
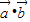 =
=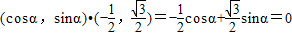 ,
,即cos(60°+α)=0,或
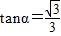 .
.因为0°≤α<360°,所以α=30°或α=210°.
点评:本题考查向量的数量积判断两个向量的垂直关系,考查了数学转化思想方法,训练了三角函数的已知三角函数值求角的方法,考查了学生的计算能力,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°), =(-
=(- ,
, ).
).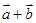 与
与 垂直;
垂直; 与
与 的模相等时,求角α.
的模相等时,求角α.