题目内容
已知函数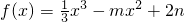
（m，n为常数），当x=2时，函数f（x）有极值，若函数f（x）只有三个零点，则实数n的取值范围是
- A.
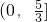
- B.
- C.
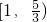
- D.
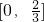
B
分析：先求导，由于当x=2时，函数f（x）有极值，可得f′（2）=22-4m=0，解得m的值．令f′（x）=0，解得x=0或2，列表如下，由表格即可得到函数f（x）的极大值和极小值．
函数f（x）只有三个零点?
，解出即可．
解答：f′（x）=x2-2mx，∵当x=2时，函数f（x）有极值，∴f′（2）=22-4m=0，解得m=1．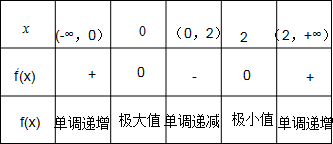
∴f′（x）=x2-2x=x（x-2），经验证x=2时函数f（x）有极值．
令f′（x）=0，解得x=0或2，列表如下：
由表格可知：当x=0时，函数f（x）取得极大值，且[f（x）]极大值=f（0）=2n；
当x=2时，函数f（x）取得极小值，且[f（x）]极小值=f（2）=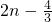
．
∵函数f（x）只有三个零点，∴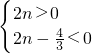
，解得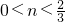
．
∴实数n的取值范围是．
故选B．
点评：熟练掌握利用导数研究函数的单调性、极值及函数f（x）只有三个零点?是解题的关键．
分析：先求导，由于当x=2时，函数f（x）有极值，可得f′（2）=22-4m=0，解得m的值．令f′（x）=0，解得x=0或2，列表如下，由表格即可得到函数f（x）的极大值和极小值．
函数f（x）只有三个零点?
，解出即可．解答：f′（x）=x2-2mx，∵当x=2时，函数f（x）有极值，∴f′（2）=22-4m=0，解得m=1．
∴f′（x）=x2-2x=x（x-2），经验证x=2时函数f（x）有极值．
令f′（x）=0，解得x=0或2，列表如下：
由表格可知：当x=0时，函数f（x）取得极大值，且[f（x）]极大值=f（0）=2n；
当x=2时，函数f（x）取得极小值，且[f（x）]极小值=f（2）=
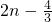．∵函数f（x）只有三个零点，∴
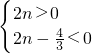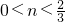，解得．∴实数n的取值范围是
．故选B．
点评：熟练掌握利用导数研究函数的单调性、极值及函数f（x）只有三个零点?
是解题的关键． 
练习册系列答案
相关题目
在[m，n]（m＜n）上的最小值为t，若t≤m恒成立，则称函数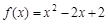
在[1，2]上是否具有“DK”性质，说明理由；
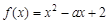在[a，a＋1]上具有“DK”性质，求a的取值范围．
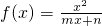（m，n为常数），且关于x的方程f（x）=x-12有两个实数根x1=3，x2=4．
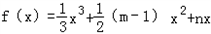（m、n为常数）．
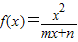（m，n为常数），且关于x的方程f（x）=x-12有两个实数根x1=3，x2=4．