Question

（2012•佛山二模）已知椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的一个焦点为F₁（-

3

，0），而且过点H（

3

，

1

2

）．
（1）求椭圆E的方程；
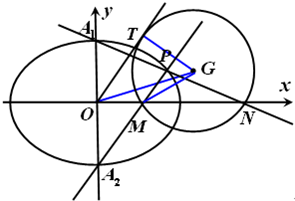
（2）设椭圆E的上下顶点分别为A₁，A₂，P是椭圆上异于A₁，A₂的任一点，直线OT与过点M，N的圆G相切，切点为G．证明：线段OT的长为定值．

Answer 1

分析：（1）利用椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的一个焦点为F₁（-

3

，0），而且过点H（

3

，

1

2

），建立方程，即可求得椭圆E的方程；
（2）先计算|OM|•|ON|，再利用切割线定理可得线段OT的长度．

解答：（1）解：由题意，得：

a2-b2=3 3 a2 + 1 4 b2 =1

，∴

a2=4 b2=1

∴椭圆E的方程为

x2

4

+y2=1；
（2）证明：由（1）可知A₁（0，1），A₂（0，-1），设P（x₀，y₀），
直线PA₁：y-1=

y0-1

x0

x，令y=0，得xN=

-x0

y0-1

；
直线PA₂：y+1=

y0+1

x0

x，令y=0，得xM=

-x0

y0+1

；
则|OM|•|ON|=|

-x0

y0-1

|×|

-x0

y0+1

|=

x02

y02-1

，
∵

x02

4

+y02=1，
∴|OM|•|ON|=4，由切割线定理得|OT|²=|OM|•|ON|=4
所以|OT|=2，即线段OT的长度为定值2．

点评：本题考查椭圆的标准方程，考查圆与椭圆为综合，考查线段长的求解，认真审题，挖掘隐含是关键．