题目内容
【题目】已知
为坐标原点，抛物线
，点
，设直线
与
交于不同的两点
、
.
（1）若直线
轴，求直线
的斜率的取值范围；
（2）若直线不垂直于
轴，且
，证明：直线过定点.
【答案】（1）
； （2）见解析.
【解析】
（1）先设点P在第一象限时，设出点P的坐标，利用斜率坐标公式，将PA的斜率表示出来，之后对式子进行变形，利用基本不等式求得其范围，从而得到直线PA的斜率的取值范围，同理可得点P落在第四象限时，其斜率的取值范围，之后取并集得到结果.
（2）设出直线的方程，将直线方程与抛物线方程联立，利用韦达定理求得两根的关系，利用两个角的关系，得到两条直线的斜率是互为相反数的，从而得到
，代入直线方程，求得直线过的定点.
（1）当点
在第一象限时，设
，
，
∴
，同理，当点在第四象限时，∴
，综上所述
∴
（2）设直线
的方程为
，联立方程
，得
，
，
设
，
，
，
，
∵
∴
，，
∴
，∴直线恒过定点
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据
|
|
|
|
|
|
|
|
|
|
（1）请根据上表提供的数据，用最小二乘法求出关于
的线性回归方程
；
（2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(附:
，
，
，
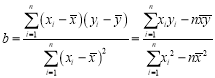，其中
,
为样本平均值)
【题目】某企业三月中旬生产
，
，
三种产品共3000件，根据分层随机抽样的结果，企业统计员制作了如下的统计表格：
产品类别 |
|
|
|
产品数量 | 1300 | ||
样本中的数量 | 130 |
由于不小心，表格中，产品的有关数据已被污染得看不清楚，统计员只记得样本中产品的数量比样本中产品的数量多10.根据以上信息，求该企业生产产品的数量.
