题目内容
已知函数 .
.
(Ⅰ) 求 的单调区间;
的单调区间;
(Ⅱ) 求所有的实数 ,使得不等式
,使得不等式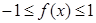 对
对 恒成立.
恒成立.
【答案】
(Ⅰ)当a≤0时, f (x)的增区间是(-∞,+∞);当a>0时,f (x)的增区间是(-∞,-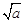 ]、[
]、[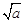 ,+∞),f (x)的减区间是[-
,+∞),f (x)的减区间是[-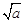 ,
,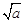 ];(Ⅱ)
];(Ⅱ)
【解析】
试题分析:(Ⅰ)本小题首先求函数的导数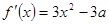 ,利用导数的正负求解原函数的单调区间,注意参数
,利用导数的正负求解原函数的单调区间,注意参数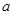 的范围,通过分情况讨论可以分别得出函数
的范围,通过分情况讨论可以分别得出函数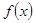 的增减区间;(Ⅱ)根据第一问可知函数
的增减区间;(Ⅱ)根据第一问可知函数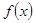 在区间
在区间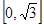 上的单调性,进而可以求得函数
上的单调性,进而可以求得函数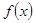 在区间
在区间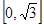 上的的最大值和最小值,然后让
上的的最大值和最小值,然后让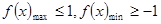 ,即可解得参数
,即可解得参数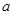 的取值范围.
的取值范围.
试题解析:(Ⅰ) f ′(x)=3x2-3a.
当a≤0时,f ′(x)≥0恒成立,故f (x)的增区间是(-∞,+∞).
当a>0时,由f ′(x)>0,得
x<-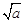 或 x>
或 x>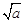 ,
,
故f (x)的增区间是(-∞,-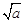 ]和[
]和[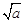 ,+∞),f (x)的减区间是[-
,+∞),f (x)的减区间是[-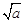 ,
,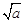 ]. 7分
]. 7分
(Ⅱ) 当a≤0时,由(Ⅰ)知f (x)在[0,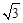 ]上递增,且f (0)=1,此时无解.
]上递增,且f (0)=1,此时无解.
当0<a<3时,由(Ⅰ)知f (x)在[0,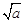 ]上递减,在[
]上递减,在[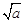 ,
,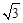 ]上递增,
]上递增,
所以f (x)在[0,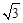 ]上的最小值为f (
]上的最小值为f (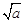 )=1-2a
)=1-2a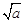 .
.
所以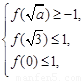
即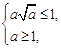
所以a=1.
当a≥3时,由(Ⅰ)知f (x)在[0,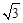 ]上递减,又f (0)=1,所以
]上递减,又f (0)=1,所以
f (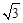 )=3
)=3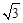 -3
-3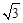 a+1≥-1,
a+1≥-1,
解得a≤1+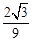 ,此时无解.
,此时无解.
综上,所求的实数a=1. 15分
考点:1.导数判断单调性;2.解不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|