Question

已知x，y满足约束条件

y≥2|x| x+y-1≤0

，若函数z=y-ax（a＞0）的最大值为3，则实数a的值为（　　）

A．1

B．4

C．2

D．3

Answer 1

分析：作出x、y满足约束条件

y≥2|x| x+y-1≤0

的图象，由图象判断出最优解，令目标函数值为3，列出a的方程，求解即可．

解答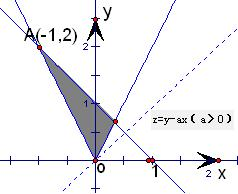：解：由题意、y满足约束条件

y≥2|x| x+y-1≤0

的图象如图
目标函数z=y-ax（a＞0）的最大值为3
从图象上知，
若函数z=y-ax（a＞0）的最大值为3，最优解是A（-1，2）
故有2-（-1）×a=3
则a=1
故选A．

点评：本题考查简单线性规划的应用及不等式的应用，解决本题，关键是根据线性规划的知识判断出取最值时的位置，即最优解，由此得到参数的方程，再构造出积为定值的形式求出真数的最小值．