题目内容
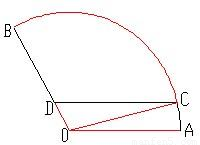
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为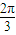 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,(1)用θ表示CD的长度,并写出θ的取值范围.
(2)当θ为何值时,观光道路最长?
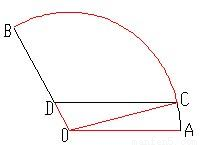
【答案】分析:(1)利用θ表示CD的长度的关键是在△COD中正确利用正弦定理;
(2)首先将道路长度L(θ)表达成θ的函数关系式,再利用导数方法研究函数的最大值,从而可以求得θ= 时,观光道路最长..
时,观光道路最长..
解答:解:(1)在△COD中,由正弦定理得 ,又CD∥AO,CO=1,∠AOC=θ,所以
,又CD∥AO,CO=1,∠AOC=θ,所以
因为OD<OB,所以 ,所以
,所以 ,所以
,所以
 ,θ的取值范围为
,θ的取值范围为
(2)设道路长度L(θ),则 ,
,
由L′(θ)=0得 ,又
,又 ,所以
,所以
易得 时,L(θ)取到最大值,即θ=
时,L(θ)取到最大值,即θ= 时,观光道路最长.
时,观光道路最长.
点评:解决实际问题的关键在于建立数学模型和目标函数,把“问题情境”译为数学语言,找出问题的主要关系,并把问题的主要关系抽象成数学问题,在数学领域寻找适当的方法解决,再返回到实际问题中加以说明.
(2)首先将道路长度L(θ)表达成θ的函数关系式,再利用导数方法研究函数的最大值,从而可以求得θ=
 时,观光道路最长..
时,观光道路最长..解答:解:(1)在△COD中,由正弦定理得
 ,又CD∥AO,CO=1,∠AOC=θ,所以
,又CD∥AO,CO=1,∠AOC=θ,所以
因为OD<OB,所以
 ,所以
,所以 ,所以
,所以 ,θ的取值范围为
,θ的取值范围为
(2)设道路长度L(θ),则
 ,
,
由L′(θ)=0得
 ,又
,又 ,所以
,所以
易得
 时,L(θ)取到最大值,即θ=
时,L(θ)取到最大值,即θ= 时,观光道路最长.
时,观光道路最长.点评:解决实际问题的关键在于建立数学模型和目标函数,把“问题情境”译为数学语言,找出问题的主要关系,并把问题的主要关系抽象成数学问题,在数学领域寻找适当的方法解决,再返回到实际问题中加以说明.

练习册系列答案
相关题目
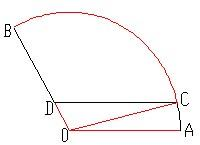 如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,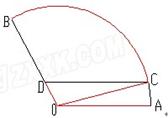
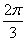 ,半径OA为1km。为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段BD组成,其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1km。为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段BD组成,其中D在线段OB上,且CD∥AO,设∠AOC=θ,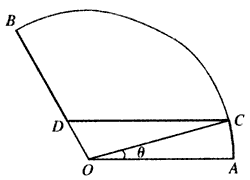
 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,