题目内容
已知对任意x∈R,不等式 >
> x2-mx+m+1恒成立,求实数m的取值范围.
x2-mx+m+1恒成立,求实数m的取值范围.
解:由题知:不等式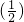 x2+x>
x2+x> x2-mx+m+1对x∈R恒成立,
x2-mx+m+1对x∈R恒成立,
∴x2+4(m+1)x-4(m+1)>0对x∈R恒成立.
∴16(m+1)2+16(m+1)<0
解得-2<x<-1
分析:将不等式变形,得到二次不等式恒成立,二次项的系数为正,判别式小于0.
点评:本题考查等价转化的能力、解决二次不等式恒成立常结合二次函数的图象从开口方向、判别式上考虑.
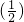 x2+x>
x2+x> x2-mx+m+1对x∈R恒成立,
x2-mx+m+1对x∈R恒成立,∴x2+4(m+1)x-4(m+1)>0对x∈R恒成立.
∴16(m+1)2+16(m+1)<0
解得-2<x<-1
分析:将不等式变形,得到二次不等式恒成立,二次项的系数为正,判别式小于0.
点评:本题考查等价转化的能力、解决二次不等式恒成立常结合二次函数的图象从开口方向、判别式上考虑.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
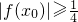 成立.
成立.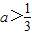
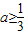
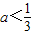
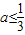
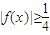 成立.
成立.