题目内容
已知对任意m∈R,直线x+y+m=0都不是f(x)=x3-3ax(a∈R)的切线.(I)求a的取值范围;
(II)求证在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
| 1 | 4 |
分析:(I)求出f(x)导函数的值域,由直线x+y+m=0都不是f(x)=x3-3ax的切线得到-1不属于导函数的值域,得到关于a的不等式,求出解集得到a的取值范围即可;
(II)要证的问题等价于当x∈[-1,1]时,|f(x)|max≥
,设g(x)=|f(x)|,g(x)在x∈[-1,1]上是偶函数,故只要证明当x∈[0,1]时,|f(x)|max≥
,分a小于等于0和a大于0小于
两种情况,讨论f'(x)的正负化简绝对值并得到函数的增减区间,根据函数的增减性分别求出|f(x)|的最小值比
大得证.
(II)要证的问题等价于当x∈[-1,1]时,|f(x)|max≥
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
解答:解:(I)f'(x)=3x2-3a∈[-3a,+∞),
∵对任意m∈R,直线x+y+m=0都不是y=f(x)的切线,
∴-1∉[-3a,+∞),-1<-3a,实数a的取值范围是a<
;
(II)证明:在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
成立等价于当x∈[-1,1]时,|f(x)|max≥
,
设g(x)=|f(x)|,g(x)在x∈[-1,1]上是偶函数,故只要证明当x∈[0,1]时,|f(x)|max≥
,
①当a≤0时,f'(x)≥0,f(x)在[0,1]上单调递增且f(0)=0,g(x)=f(x),g(x)max=f(1)=1-3a>1>
;
②当0<a<
时,f′(x)=3x2-3a=3(x+
)(x-
),列表:
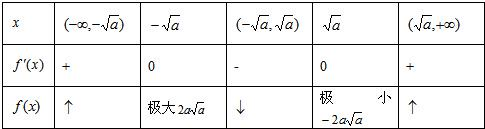
f(x)在(0,
)上递减,在(
,1)上递增,
∵
<
<1,
∴x∈(0,
)时,g(x)=-f(x),x∈(
,1)时,g(x)=f(x),
∴g(x)min=min{f(1),-f(
)},
若-f(
)>f(1)=1-3a,即
<a≤
,则g(x)max=-f(
)=2a
>
若-f(
)≤f(1)=1-3a,即0<a<
,则g(x)max=f(1)=1-3a>
;
∴在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
成立.
∵对任意m∈R,直线x+y+m=0都不是y=f(x)的切线,
∴-1∉[-3a,+∞),-1<-3a,实数a的取值范围是a<
| 1 |
| 3 |
(II)证明:在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
| 1 |
| 4 |
| 1 |
| 4 |
设g(x)=|f(x)|,g(x)在x∈[-1,1]上是偶函数,故只要证明当x∈[0,1]时,|f(x)|max≥
| 1 |
| 4 |
①当a≤0时,f'(x)≥0,f(x)在[0,1]上单调递增且f(0)=0,g(x)=f(x),g(x)max=f(1)=1-3a>1>
| 1 |
| 4 |
②当0<a<
| 1 |
| 3 |
| a |
| a |
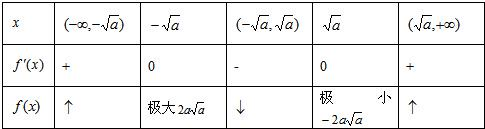
f(x)在(0,
| a |
| a |
∵
| a |
| 3a |
∴x∈(0,
| 3a |
| 3a |
∴g(x)min=min{f(1),-f(
| a |
若-f(
| a |
| 1 |
| 4 |
| 1 |
| 3 |
| a |
| a |
| 1 |
| 4 |
若-f(
| a |
| 1 |
| 4 |
| 1 |
| 4 |
∴在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
| 1 |
| 4 |
点评:此题是一道综合题,要求学生会利用导数求曲线上某点切线方程的斜率,掌握不等式恒成立时所取的条件以及导数在最值问题中的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
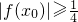 成立.
成立.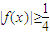 成立.
成立.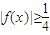 成立.
成立.