题目内容
【题目】曲线 ![]() 是平面内到定点
是平面内到定点 ![]() 的距离与到定直线
的距离与到定直线 ![]() 的距离之和为
的距离之和为 ![]() 的动点
的动点 ![]() 的轨迹.则曲线
的轨迹.则曲线 ![]() 与
与 ![]() 轴交点的坐标是________________;又已知点
轴交点的坐标是________________;又已知点 ![]() (
(![]() 为常数),那么
为常数),那么 ![]() 的最小值
的最小值 ![]() ________________.
________________.
【答案】![]()

【解析】
根据题意,求出曲线的轨迹方程,进而求出与y轴交点坐标。
通过分类讨论,在不同范围内,由曲线方程的意义求得最小值。
(1)设点P坐标为(x,y),因为动点 ![]() 到定点
到定点 ![]() 的距离与到定直线
的距离与到定直线 ![]() 的距离之和为
的距离之和为 ![]()
所以![]()
当![]() 时,代入求得
时,代入求得![]()
所以与y轴交点为![]()
(2)当![]() 时,曲线C可以化为
时,曲线C可以化为![]()
当![]() 时,曲线C可以化为
时,曲线C可以化为![]()
令![]() ,则
,则![]() 或
或![]()
解得![]() 或
或![]()
![]() 当
当![]() 或
或![]() 时,
时,![]()
所以![]()
![]() 当
当![]() 时,当直线
时,当直线![]() 与
与![]()
![]() 相交时,交点P满足
相交时,交点P满足![]() 取得最小值
取得最小值
因为抛物线准线方程为![]()
所以直线![]() 与准线交点坐标为(2,1)
与准线交点坐标为(2,1)
此时![]()
![]() 当
当![]() 时,当直线
时,当直线![]() 与
与![]()
![]() 相交时,交点P满足
相交时,交点P满足![]() 取得最小值
取得最小值
此时抛物线准线方程为![]()
所以直线![]() 与准线交点坐标为(-4,1)
与准线交点坐标为(-4,1)
此时![]()
综上所述,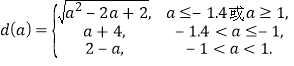

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式:
 ,
,![]() .
.
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|