题目内容

设a、b、c是某三角形的三边长,T是该三角形的面积,证明a2+b2+c2≥4T,并问何时取等号?

解：根据海伦公式T=,

要证a2+b2+c2≥成立,

只需证(a2+b2+c2)2≥3(a+b+c)·(b+c-a)(a+c-b)(a+b-c)

=3［(b+c)2-a2］［a2-(b-c)2］

=3［(2ab)2-(a2-b2-c2)2］,

即只需证a4+b4+c4≥a2b2+b2c2+c2a2,

由排序不等式,知a4+b4+c4≥a2b2+b2c2+c2a2成立.

∴原不等式成立,并当且仅当a=b=c时等号成立.

练习册系列答案
相关题目
设a，b，c是直角三角形的三边长，其中c为斜边，且c≠1，求证：log（c+b）a+log（c-b）a=2log（c+b）a•log（c-b）a．
（2012•眉山一模）设函数f（x）对其定义域内的任意实数x1与x2都有f(
x1+x2
2
)≥
f(x1)+f(x2)
2
，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有f(
x1+x2+…+xn
n
)≥
f(x1)+f(x2)+…+f(xn)
n
（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
①f（x）=lnx（x＞0）是上凸函数；
②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且
AC
=λ
CB
，则f(
x1+λx2
1+λ
)≥
f(x1)+λf(x2)
1+λ
；
④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是
3
3
2
．
其中，正确命题的序号是
①③④
①③④
（写出所有你认为正确命题的序号）．
设a、b、c是直角三角形的三边长，其中c为斜边，且c≠1.

求证：log(c+b)a+log(c-b)a=2log(c+b)a·log(c-b)a.

设函数f（x）对其定义域内的任意实数，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有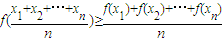（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
①f（x）=lnx（x＞0）是上凸函数；
②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且；
④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是．
其中，正确命题的序号是    （写出所有你认为正确命题的序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网