题目内容
10.已知二次方程(m-1)x2+(3m+4)x+(m+1)=0的两个根都属于(-1,1),求m的取值范围.分析 设f(x)=(m-1)x2+(3m+4)x+(m+1),则由题意利用二次函数的性质求得m的取值范围.
解答 解:设f(x)=(m-1)x2+(3m+4)x+(m+1),则由题意可得$\left\{\begin{array}{l}{△{=(3m+4)}^{2}-4(m-1)(m+1)≥0}\\{-1<\frac{3m+4}{2(1-m)}<1}\\{f(-1)•f(1)>0}\end{array}\right.$,
即 $\left\{\begin{array}{l}{{5m}^{2}+24m+20≥0}\\{\frac{5m+3}{2(m-1)}>0}\\{\frac{m+5}{2m-1}<0}\\{(-m-4)(5m+2)>0}\end{array}\right.$,求得-4<m≤$\frac{-12-2\sqrt{11}}{5}$.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
5.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+4a,x<1\\-x+1,x≥1\end{array}$是定义在R上的减函数,则a的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |
20.设a=(lg3)2,b=30.3,c=lg$\sqrt{3}$,则( )
| A. | a<c<b | B. | c<a<b | C. | b<a<c | D. | b<c<a |
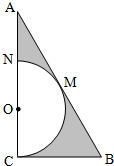 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.