题目内容
已知椭圆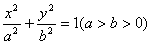 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足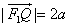 ,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足 ,
,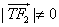 。
。
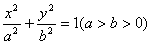 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足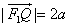 ,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足 ,
,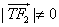 。
。
(1)设x为点P的横坐标,证明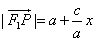 ;
;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M, 使△F1MF2的面积S=b2。若存在,求∠F1MF2的正切值;若不存在,请说明理由。
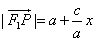 ;
; (2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M, 使△F1MF2的面积S=b2。若存在,求∠F1MF2的正切值;若不存在,请说明理由。
解:(1)设点P的坐标为
由P 在椭圆上,得
在椭圆上,得
 =
=

由 ,知
,知
所以 =
= 。
。
(2)设点T的坐标为
当 =0时,点(a,0)和点(-a,0)在轨迹上
=0时,点(a,0)和点(-a,0)在轨迹上
当| |≠0且
|≠0且 时,由
时,由 得
得
又
所以T为线段F2Q的中点
在△QF1F2中,
所以有
综上所述,点T的轨迹C的方程是 。
。
(3)C上存在点M(x0,y0)使S=b2的充要条件是

由③得
由④得
所以当 时,存在点M,使S=
时,存在点M,使S=
当 时,不存在满足条件的点M。
时,不存在满足条件的点M。
当 时,
时,
由


得 。
。

由P
 在椭圆上,得
在椭圆上,得 =
=

由
 ,知
,知
所以
 =
= 。
。(2)设点T的坐标为

当
 =0时,点(a,0)和点(-a,0)在轨迹上
=0时,点(a,0)和点(-a,0)在轨迹上当|
 |≠0且
|≠0且 时,由
时,由 得
得
又

所以T为线段F2Q的中点
在△QF1F2中,

所以有

综上所述,点T的轨迹C的方程是
 。
。(3)C上存在点M(x0,y0)使S=b2的充要条件是

由③得

由④得

所以当
 时,存在点M,使S=
时,存在点M,使S=
当
 时,不存在满足条件的点M。
时,不存在满足条件的点M。当
 时,
时,
由



得
 。
。
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线