题目内容
【题目】已知椭圆C： 
(a>b>0)的离心率为
，焦距为2c，且c， 
，2成等比数列．
(Ⅰ)求椭圆C的标准方程；
(Ⅱ)点B坐标为(0， 
)，问是否存在过点B的直线l交椭圆C于M，N两点，且满足
(O为坐标原点)？若存在，求出此时直线l的方程；若不存在，请说明理由．
【答案】(Ⅰ) 
＋y2＝1(Ⅱ)y＝
x＋
或y＝－
x＋
.
【解析】试题分析：(Ⅰ)根据题意可以知道: (
)2＝2·c ,椭圆的离心率可得a＝
,即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)设直线MN的方程,代入椭圆方程,由韦达定理及向量数量积的坐标运算,即可求得k的值,直线l的方程.
试题解析：(Ⅰ)( 
)2＝2·c，解得c＝1.
又e′＝
＝
，及a2＝b2＋c2，解得a＝
，b＝1.
所以椭圆C的标准方程为
＋y2＝1.
(Ⅱ)若直线l过点B(0， 
)．
当直线l的斜率不存在时，显然不符合题意；
故直线l的斜率存在，设为k，则直线l的方程为y－
＝kx，即y＝kx＋
.
联立方程组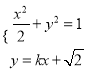
消去y，得(1＋2k2)x2＋4
kx＋2＝0.
显然Δ＝(4
k)2－4(1＋2k2)×2>0，
解得k>
或k<－
.(*)
设点M(x1，y1)，N(x2，y2)，
则x1＋x2＝
，x1x2＝
.
由
，得
＝0，则x1x2＋y1y2＝0.
即
＋(kx1＋
)(kx2＋
)＝0，得
＋k2x1x2＋
k(x1＋x2)＋2＝0，
得
＋k2·
＋
k
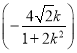＋2＝0，
化简得
＝0，解得k＝±
.符合(*)式，
此时直线l的方程为y＝
x＋
或y＝－
x＋
.
故存在过点B的直线l交椭圆C于M，N两点，且满足
，
此时直线l的方程为y＝
x＋
或y＝－
x＋
.
练习册系列答案
阅读快车系列答案
相关题目
