题目内容
【题目】定义:若各项为正实数的数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列![]() 满足
满足![]() 且
且![]() 点
点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]()
![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]()
![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)从数列![]() 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项![]() ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列![]() :
:![]() .若数列
.若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
【答案】(1) 是,理由祥见解析;(2) 证明祥见解析,![]() ;(3) k=6,m=3.
;(3) k=6,m=3.
【解析】
试题(1)利用“平方递推数列”的定义判断即可;
(2)利用(1)的结论,由等比数列的定义即可得证,进而由等比数列的通项公式即可写出通项公式![]() ;
;
(3)由无穷等比数列的各项和公式可得关于m,k的方程,由于m,k都是正整数,所以对m的取值进行分类讨论:当![]() 时代入方程可知矛盾,
时代入方程可知矛盾,![]() ,从而得到
,从而得到![]() 或2,然后再分别讨论即可求得m,k的值.
或2,然后再分别讨论即可求得m,k的值.
试题解析:(1)答:数列![]() 是算术平方根递推数列.
是算术平方根递推数列.
理由:![]() 在函数
在函数![]() 的图像上,
的图像上,
![]()
![]() ,
,![]() .
.
又![]() ,
,
∴![]() .
.
∴数列![]() 是算术平方根递推数列.
是算术平方根递推数列.
证明(2)![]() ,
,
![]() .
.
又![]() ,
,
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比
,公比![]() 的等比数列.
的等比数列.
![]() .
.
(3)由题意可知,无穷等比数列![]() 的首项
的首项![]() ,公比
,公比![]() ,
,
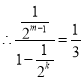 .
.
化简,得![]() .
.
若![]() ,则
,则![]() .这是矛盾!
.这是矛盾!
![]() .
.
又![]() 时,
时,![]() ,
,
![]()
![]() .
.
![]() .
.
![]()

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目