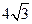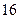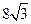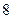题目内容
(本小题满分12分)
已知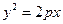
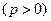 ,过点
,过点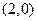 作直线与抛物线交于两点,若两点纵坐标之积为
作直线与抛物线交于两点,若两点纵坐标之积为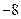 .
.
(1)求抛物线方程;
(2)斜率为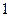 的直线不经过点
的直线不经过点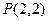 且与抛物线交于
且与抛物线交于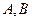
(Ⅰ)求直线 在
在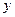 轴上截距
轴上截距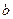 的取值范围;
的取值范围;
(Ⅱ)若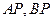 分别与抛物线交于另一点
分别与抛物线交于另一点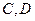 ,证明:
,证明: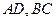 交于一定点
交于一定点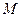 .
.
已知
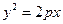
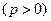 ,过点
,过点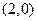 作直线与抛物线交于两点,若两点纵坐标之积为
作直线与抛物线交于两点,若两点纵坐标之积为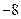 .
.(1)求抛物线方程;
(2)斜率为
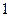 的直线不经过点
的直线不经过点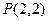 且与抛物线交于
且与抛物线交于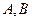
(Ⅰ)求直线
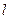 在
在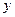 轴上截距
轴上截距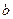 的取值范围;
的取值范围;(Ⅱ)若
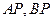 分别与抛物线交于另一点
分别与抛物线交于另一点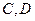 ,证明:
,证明: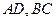 交于一定点
交于一定点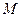 .
. 解:(1)设两交点坐标分别为
解:(1)设两交点坐标分别为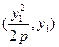 ,
,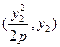 ,因直线经过点
,因直线经过点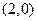 ,故有
,故有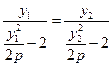 ,即
,即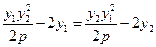 ,化简得
,化简得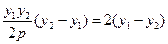 ,易知
,易知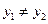
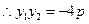 ,
,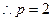 ………4分
………4分即抛物线方程为
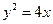
(2)(Ⅰ)将直线方程
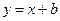 代入
代入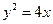 得
得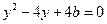 ,由
,由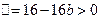 得
得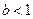 ,
,又斜率为1经过点
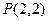 的直线截距为
的直线截距为 ,
,于是直线
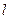 在
在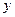 轴上截距
轴上截距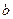 的取值范围是
的取值范围是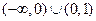 ………8分
………8分(Ⅱ)设
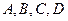 的坐标分别为
的坐标分别为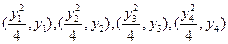 ,
,则直线
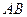 的斜率
的斜率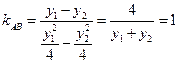 ,
,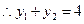
同理知直线
 的斜率分别为
的斜率分别为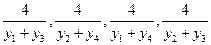
于是由
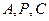 三点共线得
三点共线得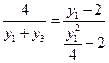 ,
,化简得
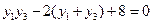 ①
①以
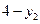 替换
替换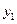 得
得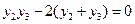 ②
②同理由
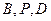 三点共线得
三点共线得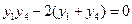
再由
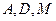 及
及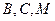 共线分别得到
共线分别得到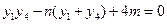 ③
③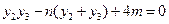 ④
④将①②式分别代入③④式得
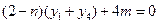
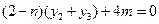
易知
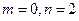 ,即
,即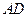 与
与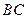 交于点
交于点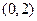 . ………12分
. ………12分略

练习册系列答案
相关题目
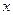 轴上的抛物线与
轴上的抛物线与 直线
直线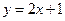 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=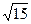 ,求抛物线的方程
,求抛物线的方程
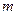 时,水面宽4
时,水面宽4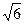
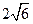
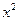 上的动点,点M到直线2x-y-a=0(a为常数)的最短距离为
上的动点,点M到直线2x-y-a=0(a为常数)的最短距离为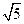 ,则实数a的值为
,则实数a的值为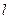 过抛物线
过抛物线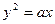 (
(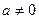 )的焦点
)的焦点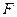 ,且和
,且和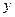 轴交于点
轴交于点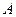 ,若
,若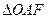 (
(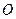 为坐标原点)的面积为4,则抛物线方程为
为坐标原点)的面积为4,则抛物线方程为 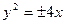
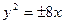
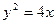
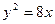
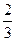 y的焦点的纵坐标与它的通径的比是
y的焦点的纵坐标与它的通径的比是 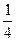
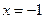 的距离的和的最小值是 。
的距离的和的最小值是 。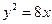 的焦点为
的焦点为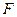 ,准线为
,准线为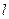 ,
,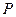 为抛物线上一点,
为抛物线上一点,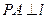 ,
,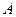 为垂足,如果直线
为垂足,如果直线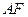 斜率为
斜率为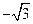 ,那么
,那么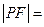 ( )
( )