题目内容
已知矩形ABCD,AB=1,BC=x,将△ABD沿矩形对角线BD所在的直线进行翻折,在翻折过程中,则
- A.?x∈(0,2),都存在某个位置,使得AB⊥CD
- B.?x∈(0,2),都不存在某个位置,使得AB⊥CD
- C.?x>1,都存在某个位置,使得AB⊥CD
- D.?x>1,都不存在某个位置,使得AB⊥CD
C
分析:利用线面垂直的判定和性质定理即可得出.
解答:建立如图所示的空间直角坐标系,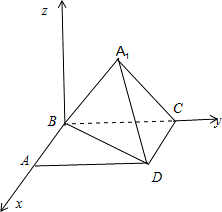 B(0,0,0),C(0,x,0),D(1,x,0).
B(0,0,0),C(0,x,0),D(1,x,0).
假设将△ABD沿矩形对角线BD所在的直线进行翻折时存在某个位置A1BD,(A1是点A翻折后的位置),使得AB⊥CD.
又∵BA1⊥A1D,∴BA1⊥平面A1CD.
设A1(a,b,c),则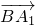 =(a,b,c),
=(a,b,c),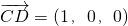 ,
, =(1-a,x-b,-c).
=(1-a,x-b,-c).
由 =0,
=0,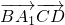 =0,得到
=0,得到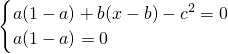 ,得到
,得到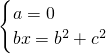 或
或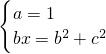 .
.
①当a=1时,此时矩形变为正方形,点A1与C重合,满足AB⊥CD;
②当a=0时,点A1位于yoz坐标平面内,此时,b2+c2=1,0<b<1,∴x=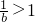 .
.
综上可知:当x≥1时,将△ABD沿矩形对角线BD所在的直线进行翻折,在翻折过程中,使得AB⊥CD.
故选C.
点评:熟练掌握线面垂直的判定和性质定理是解题的关键.
分析:利用线面垂直的判定和性质定理即可得出.
解答:建立如图所示的空间直角坐标系,
 B(0,0,0),C(0,x,0),D(1,x,0).
B(0,0,0),C(0,x,0),D(1,x,0).假设将△ABD沿矩形对角线BD所在的直线进行翻折时存在某个位置A1BD,(A1是点A翻折后的位置),使得AB⊥CD.
又∵BA1⊥A1D,∴BA1⊥平面A1CD.
设A1(a,b,c),则
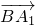 =(a,b,c),
=(a,b,c),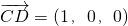 ,
, =(1-a,x-b,-c).
=(1-a,x-b,-c).由
 =0,
=0,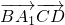 =0,得到
=0,得到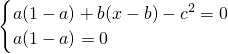 ,得到
,得到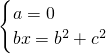 或
或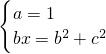 .
.①当a=1时,此时矩形变为正方形,点A1与C重合,满足AB⊥CD;
②当a=0时,点A1位于yoz坐标平面内,此时,b2+c2=1,0<b<1,∴x=
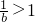 .
.综上可知:当x≥1时,将△ABD沿矩形对角线BD所在的直线进行翻折,在翻折过程中,使得AB⊥CD.
故选C.
点评:熟练掌握线面垂直的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知矩形ABCD中,
已知矩形ABCD中, 如图所示,已知矩形ABCD中,AB=
如图所示,已知矩形ABCD中,AB=