题目内容
设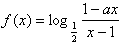 为奇函数,a为常数,
为奇函数,a为常数,
(1)求a的值;
(2)证明:f(x)在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个x的值,不等式f(x)>(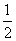 )x+m恒成立,求实数m的取值范围。
)x+m恒成立,求实数m的取值范围。
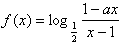 为奇函数,a为常数,
为奇函数,a为常数,(1)求a的值;
(2)证明:f(x)在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个x的值,不等式f(x)>(
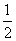 )x+m恒成立,求实数m的取值范围。
)x+m恒成立,求实数m的取值范围。 解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
∴
 ,
,
检验a=1(舍),
∴a=-1;
(2)证明:任取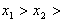 1,
1,
∴ ,
,
∴
 ,
,
即 ,
,
∴f(x)在(1,+∞)内单调递增。
(3)对于[3,4]上的每一个x的值,不等式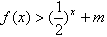 恒成立,
恒成立,
即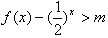 恒成立,
恒成立,
令 ,
,
只需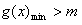 ,
,
用定义可证g(x)在[3,4]上是增函数,
∴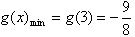 ,
,
∴ 时,原式恒成立。
时,原式恒成立。
∴f(-x)=-f(x),
∴

 ,
,检验a=1(舍),
∴a=-1;
(2)证明:任取
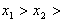 1,
1,∴
 ,
, ∴

 ,
,即
 ,
,∴f(x)在(1,+∞)内单调递增。
(3)对于[3,4]上的每一个x的值,不等式
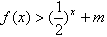 恒成立,
恒成立,即
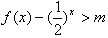 恒成立,
恒成立,令
 ,
,只需
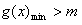 ,
,用定义可证g(x)在[3,4]上是增函数,
∴
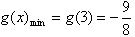 ,
,∴
 时,原式恒成立。
时,原式恒成立。 
练习册系列答案
相关题目
 为奇函数,a为常数.
为奇函数,a为常数. 恒成立,求实数m取值范围.
恒成立,求实数m取值范围. 为奇函数,a为常数。
为奇函数,a为常数。 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 为奇函数,a为常数。
为奇函数,a为常数。 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。 为奇函数, a为常数。
为奇函数, a为常数。 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。