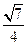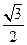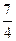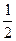题目内容
(本小题满分10分)如图,椭圆C: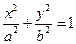 的焦距为
的焦距为 2,离心率为
2,离心率为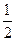 。
。
(1)求椭圆C的方程
(2)设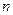 是过原点的直线,
是过原点的直线,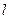 是与
是与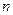 垂直相交于P点且与椭圆相交于A、B两点的直线,
垂直相交于P点且与椭圆相交于A、B两点的直线,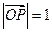 ,是否存在上述直线
,是否存在上述直线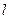 使
使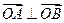 成立?若存在,求出直线
成立?若存在,求出直线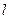 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。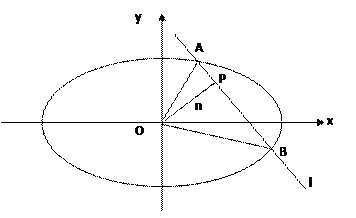
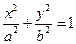 的焦距为
的焦距为 2,离心率为
2,离心率为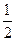 。
。(1)求椭圆C的方程
(2)设
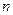 是过原点的直线,
是过原点的直线,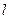 是与
是与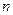 垂直相交于P点且与椭圆相交于A、B两点的直线,
垂直相交于P点且与椭圆相交于A、B两点的直线,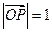 ,是否存在上述直线
,是否存在上述直线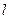 使
使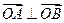 成立?若存在,求出直线
成立?若存在,求出直线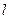 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(1)

(2)不存在直线
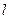 使
使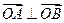 成立
成立(1)由2c=2知c=1

(2)设
假设使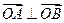 成立的直线
成立的直线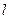 存在
存在
1)当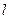 垂直于x轴时由
垂直于x轴时由
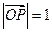 知
知

不存在直线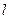 使
使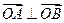 成立
成立
2)当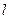 不垂直于x轴时,设
不垂直于x轴时,设
则由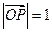 知
知
由



由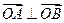 知
知
将 代入上式并化简的
代入上式并化简的 ,此方程无解
,此方程无解
故此时直线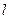 不存在
不存在
综上所诉,不存在直线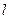 使
使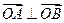 成立
成立

(2)设

假设使
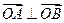 成立的直线
成立的直线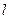 存在
存在1)当
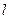 垂直于x轴时由
垂直于x轴时由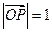 知
知

不存在直线
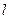 使
使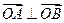 成立
成立2)当
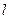 不垂直于x轴时,设
不垂直于x轴时,设
则由
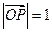 知
知
由




由
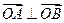 知
知
将
 代入上式并化简的
代入上式并化简的 ,此方程无解
,此方程无解故此时直线
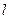 不存在
不存在综上所诉,不存在直线
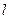 使
使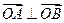 成立
成立
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
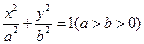 的离心率为
的离心率为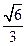 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为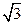 ,直线
,直线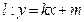 交椭圆于不同的两点
交椭圆于不同的两点 ,
,
 到直线
到直线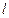 的距离为
的距离为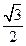 ,求
,求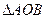 面积的最大值
面积的最大值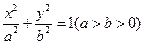 ,两个焦点分别为
,两个焦点分别为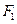 、
、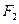 ,斜率为k的直线
,斜率为k的直线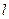 过右焦点
过右焦点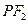 的中点恰为B。
的中点恰为B。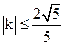 ,求椭圆C的离心率的取值范围。
,求椭圆C的离心率的取值范围。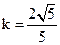 ,A、B到右准线距离之和为
,A、B到右准线距离之和为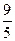 ,求椭圆C的方程。
,求椭圆C的方程。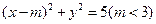 与椭圆E:
与椭圆E: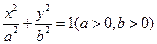 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线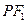 与圆C相切。
与圆C相切。
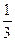 ,则椭圆方程
,则椭圆方程 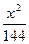 +
+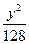 ="1"
="1"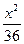 +
+ ="1"
="1"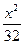 +
+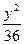 ="1"
="1"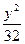 =1
=1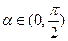 ,方程
,方程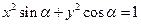 表示焦点在
表示焦点在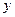 轴上的椭圆,则
轴上的椭圆,则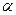 的取值范围是()
的取值范围是()
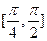
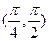
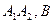 为短轴一端点,若
为短轴一端点,若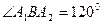 ,则椭圆的离心率为( )
,则椭圆的离心率为( )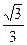
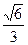
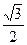
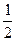
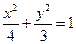 的离心率为
的离心率为