Question

【题目】已知函数f（x）＝sinx，g（x）＝lnx．

（1）求方程在[0，2π]上的解；

（2）求证：对任意的a∈R，方程f（x）＝ag（x）都有解；

（3）设M为实数，对区间[0，2π]内的满足x1＜x2＜x3＜x4的任意实数xi（1≤i≤4），不等式成立，求M的最小值．

Answer 1

【答案】（1）或；（2）详见解析；（2）

【解析】

（1）利用诱导公式化简，结合同角三角函数的基本关系式求得的值，由此求得方程的解.

（2）将分成和两种情况，结合零点存在性证得结论成立.

（3）先证得，再证得，由此求得的最小值为.

（1）因为，，所以，即，且.若，则，与矛盾.所以，从而.又，所以或.

（2）当时，由得，即是该方程的一个解；

当时，令.因为的图像在区间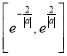上连续不断，且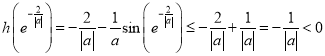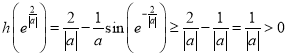，，根据零点存在性定理可知，存在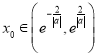，使得.因此，当时，方程有解.

综上所述，对任意，方程都有解.

（3）先证：.

取，.

再证：当时，都有，即.

①若，因为，于是，所以，而，所以.

②若，，，所以；

③若，，，所以，

于是对任意满足条件的，都有.

综上所述，的最小值为.