题目内容
我们把同时满足下列两个性质的函数称为“和谐函数”:①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间[p,q](p<q),使得函数在区间[p,q]上的值域为[p2,q2].
(1)已知幂函数f(x)的图象经过点(2,2),判断g(x)=f(x)+2(x∈R)是否是和谐函数?
(2)判断函数
 是否是和谐函数?
是否是和谐函数?(3)若函数
 是和谐函数,求实数t的取值范围.
是和谐函数,求实数t的取值范围.
【答案】分析:(1)利用幂函数f(x)的图象经过点(2,2),求出函数的表达式,然后判断g(x)=f(x)+2(x∈R)是否是和谐函数.
(2)直接利用新定义,判断函数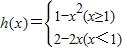 是否满足和谐函数的定义,即可推出结果;
是否满足和谐函数的定义,即可推出结果;
(3)利用新定义,函数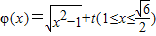 是和谐函数,推出关系式即可求实数t的取值范围.
是和谐函数,推出关系式即可求实数t的取值范围.
解答:解:(1)设f(x)=xα(α∈R),由f(2)=2α=2,得α=1,f(x)=x,g(x)=x+2在R上是增函数,
令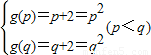 ,得p=-1,q=2
,得p=-1,q=2
故g(x)=f(x)+2是和谐函数. …(4分)
(2)易得h(x)为R上的减函数,
①若p<q<1则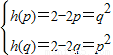 ,相减得p+q=2与p<q<1矛盾;
,相减得p+q=2与p<q<1矛盾;
②若1≤p<q则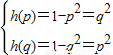 ,p2+q2=1与1≤p<q矛盾;
,p2+q2=1与1≤p<q矛盾;
③若p<1≤q则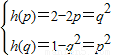 ,p=1与p<1矛盾.
,p=1与p<1矛盾.
故h(x)不是和谐函数. …(8分)
(3)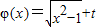 在
在 上是增函数,
上是增函数,
由函数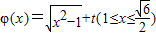 是和谐函数知,
是和谐函数知,
函数φ(x)在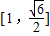 内存在区间[p,q](p<q),使得函数在区间[p,q]上的值域为[p2,q2].
内存在区间[p,q](p<q),使得函数在区间[p,q]上的值域为[p2,q2].
∴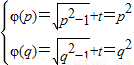
∴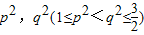 是方程
是方程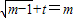 在区间
在区间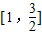 内的两个不等实根
内的两个不等实根
?x2-x+1-t=0在区间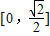 内的两个不等实根,
内的两个不等实根,
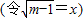
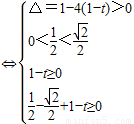
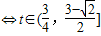 …(12分)
…(12分)
点评:本题考查新定义的理解以及应用,考查函数与方程的关系,函数的单调性与函数的定义域与函数的值域的综合应用.
(2)直接利用新定义,判断函数
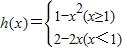 是否满足和谐函数的定义,即可推出结果;
是否满足和谐函数的定义,即可推出结果;(3)利用新定义,函数
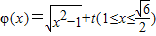 是和谐函数,推出关系式即可求实数t的取值范围.
是和谐函数,推出关系式即可求实数t的取值范围.解答:解:(1)设f(x)=xα(α∈R),由f(2)=2α=2,得α=1,f(x)=x,g(x)=x+2在R上是增函数,
令
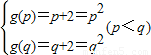 ,得p=-1,q=2
,得p=-1,q=2故g(x)=f(x)+2是和谐函数. …(4分)
(2)易得h(x)为R上的减函数,
①若p<q<1则
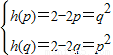 ,相减得p+q=2与p<q<1矛盾;
,相减得p+q=2与p<q<1矛盾;②若1≤p<q则
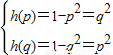 ,p2+q2=1与1≤p<q矛盾;
,p2+q2=1与1≤p<q矛盾;③若p<1≤q则
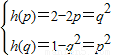 ,p=1与p<1矛盾.
,p=1与p<1矛盾.故h(x)不是和谐函数. …(8分)
(3)
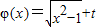 在
在 上是增函数,
上是增函数,由函数
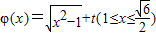 是和谐函数知,
是和谐函数知,函数φ(x)在
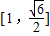 内存在区间[p,q](p<q),使得函数在区间[p,q]上的值域为[p2,q2].
内存在区间[p,q](p<q),使得函数在区间[p,q]上的值域为[p2,q2].∴
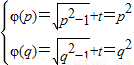
∴
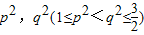 是方程
是方程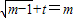 在区间
在区间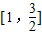 内的两个不等实根
内的两个不等实根?x2-x+1-t=0在区间
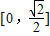 内的两个不等实根,
内的两个不等实根,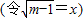
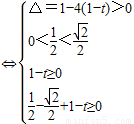
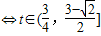 …(12分)
…(12分)点评:本题考查新定义的理解以及应用,考查函数与方程的关系,函数的单调性与函数的定义域与函数的值域的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 时,求
时,求 的反函数
的反函数 ;
; 的函数
的函数 当
当 时的最小值
时的最小值 ;
; ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间 使得函数在区间
使得函数在区间 上的值域为
上的值域为 .
. 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由; 是“和谐函数”,求实数
是“和谐函数”,求实数 的取值范围.
的取值范围. ,
, 时,求f(x)的反函数g(x);
时,求f(x)的反函数g(x); +t(x≥1)是“和谐函数”,求实数t的取值范围.
+t(x≥1)是“和谐函数”,求实数t的取值范围.