题目内容
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l的参数方程为 (t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(1)若|AB|= ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P的极坐标为( ,
, ),且满足2
),且满足2 ,求此时直线l的直角坐标方程.
,求此时直线l的直角坐标方程.
(1)倾斜角为60°或120°;(2)x-y=0或x+y-2=0.
【解析】
试题分析:(1)直线l: mx-y+1-m=0,圆C:x2+(y-1)2=5,圆心C(0, 1),半径r= ,
,
圆心C到直线l的距离d= ,
,
由|AB|=2
 =2
=2 d=
d= =
= m=±
m=± ,
,
得到直线l的斜率k=m=± ,倾斜角为60°或120°;
,倾斜角为60°或120°;
(2)得到点P(1, 1),设A(x1, y1), B(x2, y2), 由2 =
= 可得x2=3-2x1
可得x2=3-2x1
由 得(m2+1)x2-2m2x+m2-5=0,应用韦达定理及上式,得到A(
得(m2+1)x2-2m2x+m2-5=0,应用韦达定理及上式,得到A( ,
,  )
)
把点A的坐标代入圆C的方程得m=±1.
试题解析:(1)直线l: mx-y+1-m=0
圆C:x2+(y-1)2=5,圆心C(0, 1),半径r= ,
,
圆心C到直线l的距离d= ,
,
∵|AB|=2
 =2
=2 d=
d= =
= m=±
m=± ,
,
∴直线l的斜率k=m=± ,倾斜角为60°或120° 5分
,倾斜角为60°或120° 5分
(2)∵点P(1, 1),设A(x1, y1), B(x2, y2), 则
 =(1―x1, 1―y1),
=(1―x1, 1―y1),  =(x2―1, y2―1), 2
=(x2―1, y2―1), 2 =
= ,
,
∴2(1-x1)=x2-1x2=3-2x1
由 得(m2+1)x2-2m2x+m2-5=0,
得(m2+1)x2-2m2x+m2-5=0,
∴
 ,∴A(
,∴A( ,
,  )
)
把点A的坐标代入圆C的方程得m2=1 m=±1
∴直线l的方程为x-y=0或x+y-2=0 10分
考点:1.极坐标与参数方程;2.直线与圆的位置关系;3.平面向量的坐标运算.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案(本小题满分12分)某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查中,随机抽取了100名同学,相关数据如下表所示:
喜欢跑步 | 喜欢打球 | 总计 | |
男生 | 23 | 32 | 55 |
女生 | 29 | 16 | 45 |
总计 | 52 | 48 | 100 |
(1)由表中数据直观分析,喜欢打球的学生是否与性别有关?
(2)用分层抽样的方法在喜欢打球的学生中随机抽取6名,男学生应该抽取几名?
(3)在上述抽取的6名学生中任取2名,求恰有1名女学生的概率.
 的展开式中,记
的展开式中,记 项的系数为f(
项的系数为f( ,
, ),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .
),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .  为等比数列{
为等比数列{ }的前n项和,
}的前n项和, =0,则
=0,则 =( ).
=( ). 的前
的前 项和记为
项和记为 ,且
,且 ,
, ,则
,则 .
.  满足不等式组
满足不等式组 ,则
,则 的最小值是( ).
的最小值是( ). B.
B. C.
C. D.
D.
 ,若
,若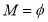 ,则实数
,则实数 的取值范围是_______________ .
的取值范围是_______________ .  是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中正确的是
是三个不同的平面,则下列命题中正确的是 B.若
B.若
 D.若
D.若