题目内容
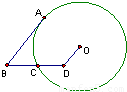
 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )分析:延长BD交圆于点E,过O作OF⊥BD,垂足为F,连OC,由切割线定理,得AB2=BC•BE,解得BE=12,CE=9,因为OF⊥CE,所以CF=
=
,DF=CF-CD=
-3=
,在直角三角形ODF中,由勾股定理,能求出⊙O的半径.
| CE |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
解答: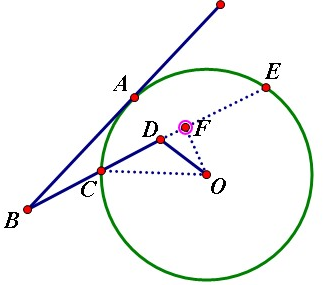 解:延长BD交圆于点E,过O作OF⊥BD,垂足为F,连OC,由切割线定理,得AB2=BC•BE,
解:延长BD交圆于点E,过O作OF⊥BD,垂足为F,连OC,由切割线定理,得AB2=BC•BE,
即62=3BE,解得BE=12,
所以CE=BE-BC=12-3=9,
因为OF⊥CE,所以CF=
=
,
所以DF=CF-CD=
-3=
,
在直角三角形ODF中,由勾股定理,得,
OF2=OD2-DF2=
,
在直角三角形OCF中,由勾股定理,得,
OC2=CF2+OF2=22,所以OC=r=
.
故选D.
 解:延长BD交圆于点E,过O作OF⊥BD,垂足为F,连OC,由切割线定理,得AB2=BC•BE,
解:延长BD交圆于点E,过O作OF⊥BD,垂足为F,连OC,由切割线定理,得AB2=BC•BE,即62=3BE,解得BE=12,
所以CE=BE-BC=12-3=9,
因为OF⊥CE,所以CF=
| CE |
| 2 |
| 9 |
| 2 |
所以DF=CF-CD=
| 9 |
| 2 |
| 3 |
| 2 |
在直角三角形ODF中,由勾股定理,得,
OF2=OD2-DF2=
| 7 |
| 4 |
在直角三角形OCF中,由勾股定理,得,
OC2=CF2+OF2=22,所以OC=r=
| 22 |
故选D.
点评:本题考查与圆有关的比例线段的应用,解题时要认真审题,仔细解答,注意勾股定理的合理运用.

练习册系列答案
相关题目
 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD=
如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD= (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为