题目内容
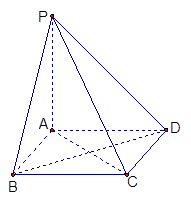
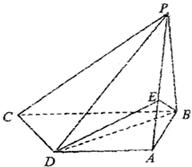
(本小题13分)如图,棱锥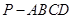 的底面
的底面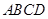 是矩形,
是矩形,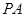 ⊥平面
⊥平面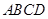 ,
,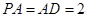 ,
,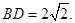
(1)求证: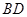 ⊥平面
⊥平面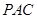 ;
;
(2)求二面角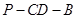 的大小;
的大小;
(3)求点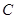 到平面
到平面 的距离.
的距离.
(1)见解析;(2)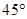 ;(3)
;(3)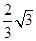
解析试题分析:(方法一)证明:(1)在 中,
中,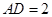 ,
,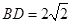 ,
,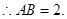
所以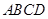 为正方形,因此
为正方形,因此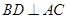 . ∵
. ∵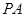 ⊥平面
⊥平面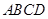 ,
,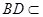 平面
平面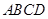 ,
,
∴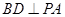 .又∵
.又∵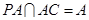 , ∴
, ∴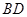 ⊥平面
⊥平面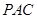 . ……4分
. ……4分
(2)解:由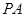 ⊥平面
⊥平面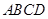 ,知
,知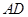 为
为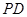 在平面
在平面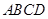 内的射影,
内的射影,
又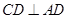 ,∴
,∴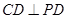 ,知
,知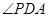 为二面角
为二面角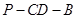 的平面角.
的平面角.
又∵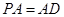 ,∴
,∴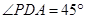 . ……9分
. ……9分
(3)∵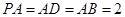 ,∴
,∴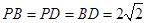 ,
,
设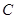 到面
到面 的距离为
的距离为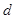 ,
,
由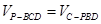 ,有
,有 ,
,
即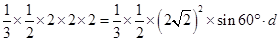 ,
,
得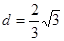 . ……14分
. ……14分
(方法二)证明:(Ⅰ)建立如图所示的直角坐标系,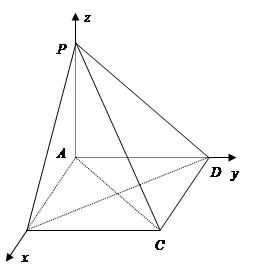
则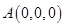 、
、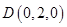 、
、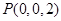 .
.
在 中,
中,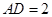 ,
,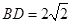 ,
,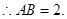 ∴
∴ ,
,
∴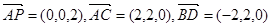 ∵
∵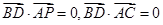 ,
,
即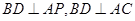 ,又∵
,又∵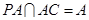 , ∴
, ∴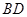 ⊥平面
⊥平面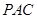 . ……4分
. ……4分
解:(2)由(Ⅰ)得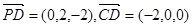 .
.
设平面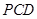 的法向量为
的法向量为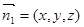 ,则
,则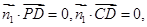
即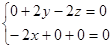 ,∴
,∴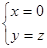 故平面
故平面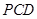 的法向量可取为
的法向量可取为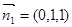

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为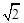 .M为线段PC的中点.
.M为线段PC的中点.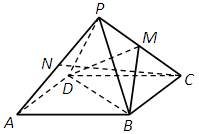
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
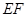 ⊥平面
⊥平面 ,
,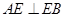 ,
,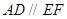 ,
,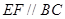 ,
,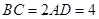 ,
,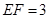 ,
,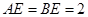 ,
,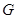 是
是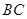 的中点.
的中点.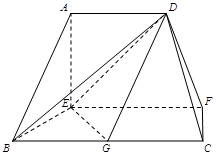
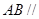 平面
平面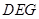 ;
;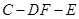 的余弦值.
的余弦值.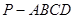 中,
中,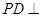 平面
平面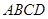 ,
,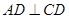 ,
,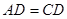 ,
,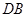 平分
平分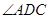 ,
,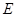 为
为 的中点.
的中点.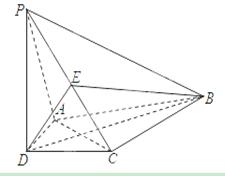
 平面
平面 ;
;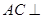 平面
平面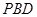 .
.
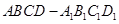 中,
中,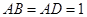 ,
,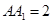 ,
,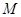 是棱
是棱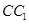 上一点,
上一点,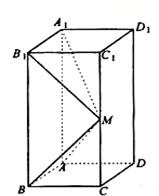
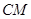 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。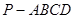 中,底面
中,底面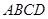 为平行四边形,
为平行四边形,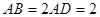 ,
,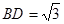 ,
,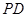 ⊥底面
⊥底面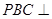 平面
平面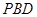 ; ②若二面角
; ②若二面角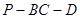 为
为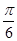 ,求
,求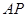 与平面
与平面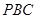 所成角的正弦值.
所成角的正弦值.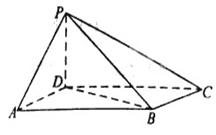
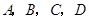 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形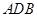 以
以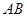 为轴运动.
为轴运动.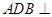 平面
平面 时,求
时,求 ;
;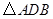 转动时,证明总有
转动时,证明总有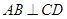 ?
?
 中,
中, ,
,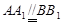 ,
, ,
, 。
。
 ;
; ;
; 的余弦值。
的余弦值。